%run ../initscript.py
HTML("""
<div id="popup" style="padding-bottom:5px; display:none;">
    <div>Enter Password:</div>
    <input id="password" type="password"/>
    <button onclick="done()" style="border-radius: 12px;">Submit</button>
</div>
<button onclick="unlock()" style="border-radius: 12px;">Unclock</button>
<a href="#" onclick="code_toggle(this); return false;">show code</a>
""")

Enter Password:

Submit

Unclock show code

%run ../../notebooks/loadtsfuncs.py
%matplotlib inline
toggle()

show code

Forecasting with Regression

Many time series follow a long-term trend except for random variation which can be modeled by regression:

\begin{equation*} Y_t = a + b t + e_t \end{equation*}

Example: Monthly US population.

df = pd.read_csv(dataurl+'Regression1.csv', parse_dates=['Month'], header=0, index_col='Month')
plot_time_series(df, 'Population', freq='', title='')

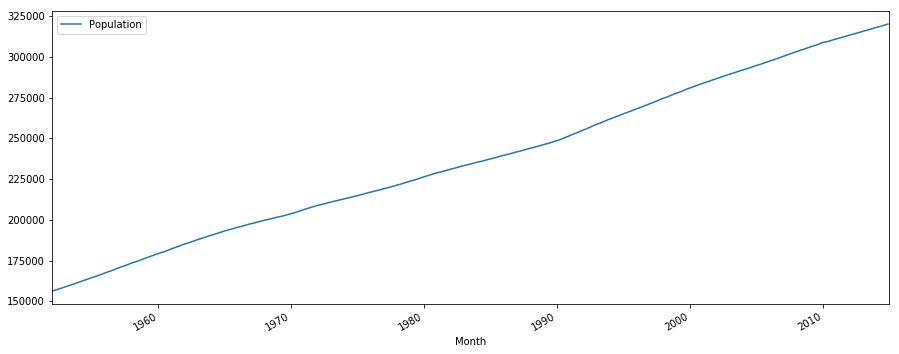
The plot indicates a clear upward trend with little or no curvature. Therefore, a linear trend is plausible.

df = pd.read_csv(dataurl+'Regression1.csv', parse_dates=['Month'], header=0, index_col='Month')
_ = analysis(df, 'Population', ['Time'], printlvl=4)

OLS Regression Results

Dep. Variable:	Population	R-squared:	0.997
Model:	OLS	Adj. R-squared:	0.997
Method:	Least Squares	F-statistic:	2.467e+05
Date:	Fri, 17 May 2019	Prob (F-statistic):	0.00
Time:	10:32:44	Log-Likelihood:	-7011.3
No. Observations:	756	AIC:	1.403e+04
Df Residuals:	754	BIC:	1.404e+04
Df Model:	1
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
Intercept	1.565e+05	188.045	832.084	0.000	1.56e+05	1.57e+05
Time	213.7755	0.430	496.693	0.000	212.931	214.620

Omnibus:	112.704	Durbin-Watson:	0.000
Prob(Omnibus):	0.000	Jarque-Bera (JB):	67.588
Skew:	-0.600	Prob(JB):	2.11e-15
Kurtosis:	2.160	Cond. No.	875.

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

standard error of estimate:2582.62518

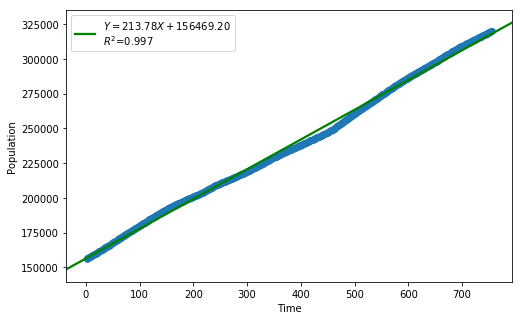
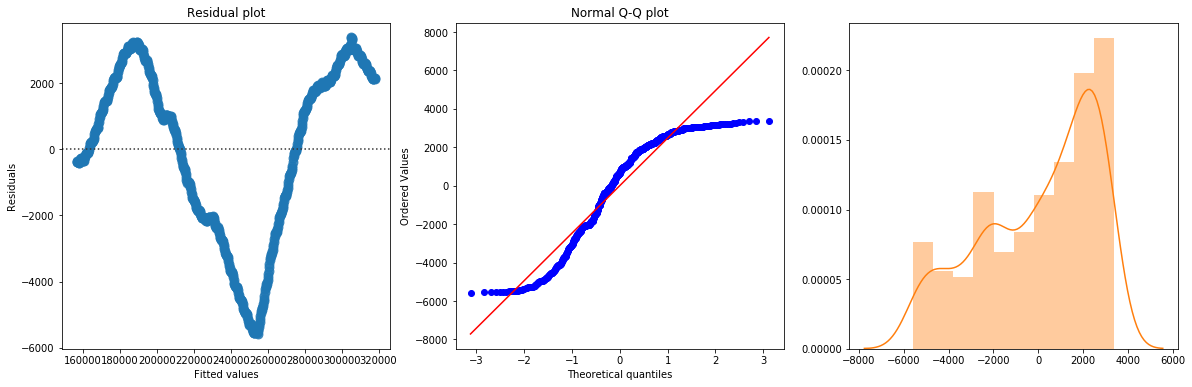
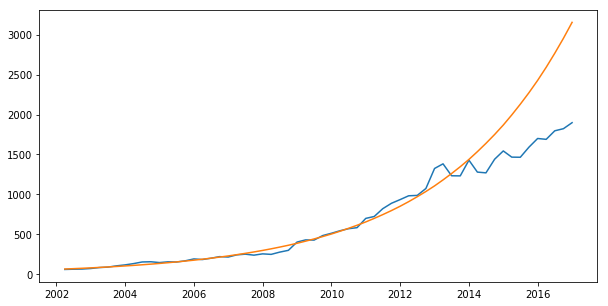
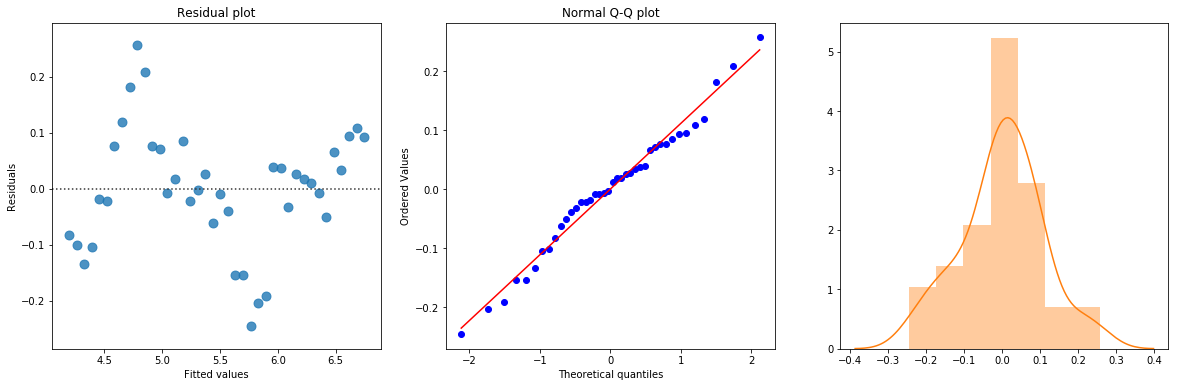
The linear fit has a very high R-squared, but is not perfect, as the residual plot indicates.

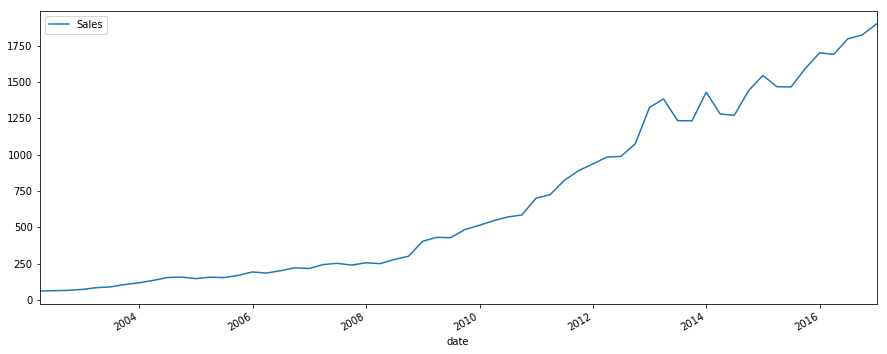
Example: Quarterly PC device sales.

df_reg = pd.read_csv(dataurl+'Regression2.csv', parse_dates=['Quarter'], header=0)
df_reg['date'] = [pd.to_datetime(''.join(df_reg.Quarter.str.split('-')[i][-1::-1]))
                       + pd.offsets.QuarterEnd(0) for i in df_reg.index]
df_reg = df_reg.set_index('date')

plot_time_series(df_reg, 'Sales', freq='', title='')

df_reg['log_sales'] = np.log(df_reg['Sales'])
df_reg[:40].tail()

	Quarter	Sales	Time	log_sales
date
2010-12-31	Q4-2010	700.19	36	6.551352
2011-03-31	Q1-2011	723.98	37	6.584764
2011-06-30	Q2-2011	821.90	38	6.711619
2011-09-30	Q3-2011	889.26	39	6.790390
2011-12-31	Q4-2011	935.33	40	6.840899

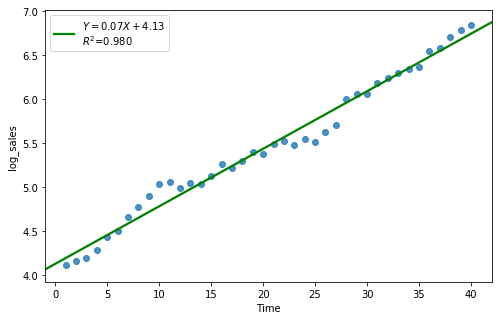
result = analysis(df_reg[:40], 'log_sales', ['Time'], printlvl=4)
df_reg['forecast'] = np.exp(df_reg['Time']*result.params[1] + result.params[0])

OLS Regression Results

Dep. Variable:	log_sales	R-squared:	0.980
Model:	OLS	Adj. R-squared:	0.980
Method:	Least Squares	F-statistic:	1871.
Date:	Fri, 17 May 2019	Prob (F-statistic):	6.24e-34
Time:	10:32:46	Log-Likelihood:	32.394
No. Observations:	40	AIC:	-60.79
Df Residuals:	38	BIC:	-57.41
Df Model:	1
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
Intercept	4.1302	0.036	116.035	0.000	4.058	4.202
Time	0.0654	0.002	43.252	0.000	0.062	0.069

Omnibus:	0.388	Durbin-Watson:	0.415
Prob(Omnibus):	0.824	Jarque-Bera (JB):	0.062
Skew:	-0.090	Prob(JB):	0.969
Kurtosis:	3.071	Cond. No.	48.0

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

standard error of estimate:0.11045

plt.subplots(1, 1, figsize=(10,5))
plt.plot(df_reg.index, df_reg.Sales, df_reg.forecast)
plt.show()