[1]:
base_dir = 'D:\\GitHub\\Optimization-and-Learning\\data\\neural_networks'
%run ../initscript.py
import pandas as pd
import numpy as np
import scipy.stats as st
import matplotlib.pyplot as plt
import seaborn as sns
from ipywidgets import *
%matplotlib inline
import tensorflow as tf
tf.logging.set_verbosity(tf.logging.ERROR)
# import sys
# sys.path.append('modules')
# import NeuralNet as nn
from keras import optimizers
from keras import backend as K
from keras import models
from keras import layers
from keras import initializers
from keras.utils import to_categorical
def sinusoidal(x):
return np.sin(np.pi * x)
def heaviside(x):
return 0.5 * (np.sign(x) + 1)
toggle()
Using TensorFlow backend.
[1]:
Neural Networks¶
The linear model takes general form \begin{align*} \mathbf{f}(\mathbf{x},\mathbf{w}) = f \left( \sum_{i=0}^{m} w_i \phi_i(\mathbf{x})\right) \end{align*}
where
\(f(\cdot)\) is a nonlinear activation function (such as \(\sigma\)) in the case of classification,
\(f(\cdot)\) is the identity in the case of regression.
Our goal is to extend this model by making the basis functions \(\phi_i(\mathbf{x})\) depend on parameters and then to allow these parameters to be adjusted, along with the coefficients \(\{w_j\}\) during training.
This leads to the basic neural network model, which can be described a series of functional transformations. Consider a two-layer network diagram:
We call it two-layer network because it is the number of layers of adaptive weights.
The network has no closed directed cycles so that outputs are deterministic functions of the inputs.
The corresponding network function is
\begin{align*} y_k(\mathbf{x},\mathbf{w}) = f \overbrace{\left( \sum_{j=0}^{\ell_2} w^{(2)}_{kj} h\underbrace{\left( \sum_{i=0}^{\ell_1} w^{(1)}_{ji} x_i\right)}_{a_j}\right)}^{a_k} \end{align*}
The quantities \(a_j\), \(a_k\) are activations. \(h(\cdot)\) is called activation function which is differentiable and nonlinear.
Due to symmetry, multiple distinct choices for the weight vector \(\mathbf{w}\) can give the same mapping function.
Keras¶
Keras is a deep-learning framework for Python that provides a convenient way to define and train almost any kind of deep-learning model.
Let’s look at an example of applying neural network on the MINST dataset to classify handwritten digits.
There is a set of 60,000 training images, plus 10,000 test images, assembled by the National Institute of Standards and Technology (NIST). Each image is a gray scale 28 \(\times\) 28 pixels handwritten digits. we’re trying to classify images into their 10 categories (0 through 9).
[2]:
from keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
print('training images:{}, test images:{}'.format(train_images.shape, test_images.shape))
training images:(60000, 28, 28), test images:(10000, 28, 28)
[3]:
def showimg(data, idx):
span = 5
if data=='train':
if idx+span<train_images.shape[0]:
images = train_images
labels = train_labels
else:
print('Index is out of range.')
if data=='test':
if idx+span<test_images.shape[0]:
images = test_images
labels = test_labels
else:
print('Index is out of range.')
plt.figure(figsize=(15,3))
for i in range(span):
plt.subplot(1, 5, i + 1)
digit = images[idx+i]
plt.imshow(digit, cmap=plt.cm.binary)
plt.title('Index:{}, Label:{}'.format(idx+i, labels[idx+i]), fontsize = 12)
plt.show()
toggle()
[3]:
[4]:
interact(showimg,
data = widgets.RadioButtons(options=['train', 'test'],
value='train', description='Data:', disabled=False),
idx = widgets.IntText(value=7, description='Index:', disabled=False));
Network Architecture¶
Tensors are fundamental to the data representations for neural networks — so fundamental that Google’s TensorFlow was named after them.
Scalars: 0 dimensional tensors
Vectors: 1 dimensional tensors
Matrix: 2 dimensional tensors
Let’s make data tensors more concrete with real-world examples:
Vector data — 2D tensors of shape (samples, features)
Timeseries data or sequence data — 3D tensors of shape (samples, timesteps, features)
Images — 4D tensors of shape (samples, height, width, channels) or (samples, channels, height, width)
Video — 5D tensors of shape (samples, frames, height, width, channels) or (samples, frames, channels, height, width)
The core building block of neural networks is the layer, a data-processing module working as a filter for data. Specifically, layers extract representations out of the data fed into them in a more useful form which is often called features.
Most of deep learning consists of chaining together simple layers that will implement a form of progressive data distillation. A deep-learning model is like a sieve for data processing, made of a succession of increasingly refined data filters the layers.
network = models.Sequential()
network.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,)))
network.add(layers.Dense(10, activation='softmax'))
Here, our network consists of a sequence of two densely connected (fully connected) layers. The second (and last) layer is a 10-way softmax layer, which means it will return an array of 10 probability scores (summing to 1). Each score will be the probability that the current digit image belongs to one of our 10 digit classes.
Compilation¶
Before training the network, we need to perform a compilation step by setting up:
An optimizer: the mechanism to improve its performance on the training data
A loss function: the measurement of its performance on the training data
Metrics to monitor during training and testing
network.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
Data Preparation¶
Before training, we preprocess our data by reshaping and scaling it. We also need to categorically encode the labels so that
[5]:
train_images_reshape = train_images.reshape((60000, 28 * 28))
train_images_reshape = train_images_reshape.astype('float32') / 255
test_images_reshape = test_images.reshape((10000, 28 * 28))
test_images_reshape = test_images_reshape.astype('float32') / 255
train_labels_cat = to_categorical(train_labels)
test_labels_cat = to_categorical(test_labels)
Training the Network¶
We train the network as follows
network.fit(train_images_reshape, train_labels_cat, epochs=5, batch_size=128, verbose=1);
The network will start to iterate on the training data in mini-batch of 128 samples, 5 times over (each iteration over all the training data is called an epoch). At each iteration, the network will compute the gradient of the weights with regard to the loss on the batch, and update the weights accordingly. After these 5 epochs, the network will have performed 2345 = 5 \(\times\) ceil(60000 \(\div\) 128) gradient updates.
Batch size impacts learning significantly. If your batch size is big enough, this will provide a stable enough estimate of what the gradient of the full dataset would be. By taking samples from your dataset, you estimate the gradient while reducing computational cost significantly.
The lower you go, the less accurate your estimate will be, however in some cases these noisy gradients can actually help escape local minimum. When it is too low, your network weights can just jump around if your data is noisy and it might be unable to learn or it converges very slowly, thus negatively impacting total computation time.
[6]:
def train_MNIST():
# We can run this function to see the trainning output.
model = models.Sequential()
model.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,)))
model.add(layers.Dense(10, activation='softmax'))
model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy'])
model.fit(train_images_reshape, train_labels_cat, epochs=5, batch_size=128, verbose=1);
model.save(base_dir+"\\minst.h5")
toggle()
[6]:
[7]:
model = models.load_model(base_dir+"\\minst.h5")
test_loss, test_acc = model.evaluate(test_images_reshape, test_labels_cat)
print('Test accuracy is {}%'.format(round(test_acc*100,2)))
10000/10000 [==============================] - 0s 48us/step
Test accuracy is 97.99%
The test set accuracy turns out to be 97.99%
Prediction¶
We perform prediction on the test dataset.
[8]:
def misclassifiedimg(index):
predicted = model.predict_classes(test_images_reshape)
result = abs(predicted - test_labels)
misclassified = np.where(result>0)[0]
print('Total number of misclassified images is {}'.format(misclassified.shape[0]),
'Examples of misclassified images {}-{}'.format(index, index+4))
plt.figure(figsize=(13,3))
for i in range(5):
plt.subplot(1, 5, i + 1)
idx = misclassified[i+index]
digit = test_images[idx]
plt.imshow(digit, cmap=plt.cm.binary)
plt.title('Predicted:{}, Label:{}'.format(predicted[idx], test_labels[idx]), fontsize = 12)
plt.show()
toggle()
[8]:
[9]:
interact(misclassifiedimg, index = widgets.IntText(value=7, description='Index:', disabled=False));
[10]:
K.clear_session()
del model
Feedfoward Neural Networks¶
Feedfoward Neural Networks (Deep feedforward networks, multilayer perceptrons (MLPs)) are the quintessential deep learning models. We demonstrate the capability of a two-layer network to model a broad range of functions, such as \(x^2\), \(\sin(x)\), \(\text{abs}(x)\) and \(\text{heaviside}(x)\).
[11]:
def create_data(func, n=50):
x = np.linspace(-1, 1, n)[:, None]
return x, func(x)
func_list = [np.square, sinusoidal, np.abs, heaviside]
def train_feedfowardNN():
for i, func in enumerate(func_list):
x_train, y_train = create_data(func)
model = models.Sequential()
model.add(layers.Dense(3, activation='tanh', input_shape=(1,), name='mid_layer'))
model.add(layers.Dense(1))
model.compile(optimizer='Adam', loss='mean_squared_error', metrics=['mse'])
model.fit(x_train, y_train, epochs=10000, batch_size=1, verbose=0);
y = model.predict(x_test)
intermediate_output = models.Model(inputs=model.input,
outputs=model.get_layer('mid_layer').output).predict(x_test)
df = pd.DataFrame(data=np.concatenate((y, intermediate_output), axis=1),
columns=['y', 'unit1', 'unit2', 'unit3'])
df.to_csv(base_dir+'\\results_{}.csv'.format(i), header=True, index=False)
K.clear_session()
del model
toggle()
[11]:
The prediction results and outputs for 3 hidden units are shown in the graph.
[12]:
x_test = np.linspace(-1, 1, 1000)
plt.figure(figsize=(12, 9))
for i, func in enumerate(func_list):
plt.subplot(2, 2, i+1)
x_train, y_train = create_data(func)
df = pd.read_csv(base_dir+'\\results_{}.csv'.format(i))
plt.title("func = {}".format(func.__name__))
plt.scatter(x_train, y_train, s=5, label='func')
plt.plot(x_test, df.y, color="r", label='fitting')
for j in range(3):
plt.plot(x_test, df['unit'+str(j+1)], linestyle='dashed', label=r"hidden unit-{}".format(j))
plt.legend(bbox_to_anchor=(1.02, 0.55), loc=2, borderaxespad=0.5)
plt.show()
toggle()
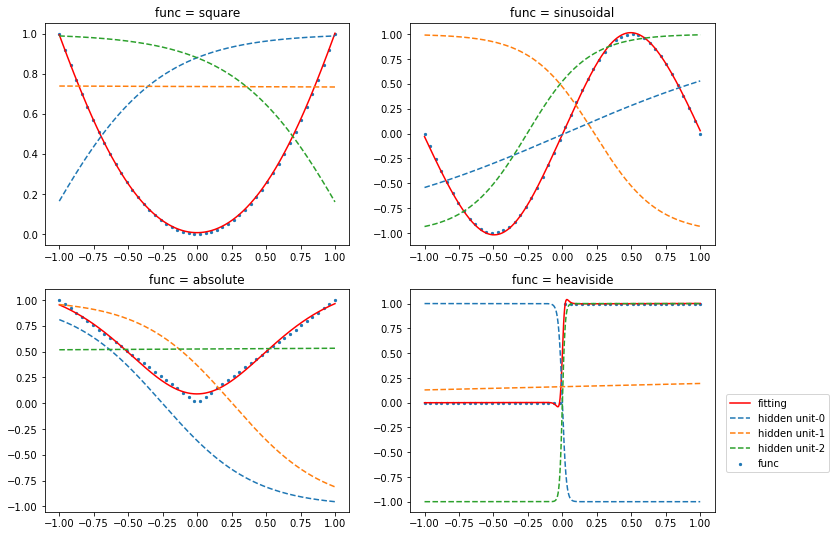
[12]:
Network Training¶
We minimize the error function (generally nonconvex) \begin{align*} E(\mathbf{w}) = \frac{1}{2} \sum_{i=1}^{n} \lVert \mathbf{f}(\mathbf{x}_i, \mathbf{w}) - \mathbf{y}_i \rVert^2 = \sum_{i=1}^{n} E_i(\mathbf{w}) \end{align*}
Error Backpropagation is applied to derive \(\frac{\partial E_i}{\partial w_{ji}}\):
Apply an input vector \(\mathbf{x}_n\) to the network and forward propagate through the network to find the activations of all the hidden and output units where
\begin{align*} z_j = h(a_j), \text{ and } a_j = \sum_i w_{ji} z_i \end{align*}
In the recursion, \(z_i = x_i\) for the input and \(z_j = y_k\) for the output.
Evaluate \(\delta_k = y_k - t_k\) for all the output units where
\begin{align*} \delta_j \equiv \frac{\partial E_i}{\partial a_j} \end{align*}
Obtain \(\delta_j\) for each hidden unit in the network by backpropagation: \begin{align*} \delta_j \equiv \frac{\partial E_i}{\partial a_j} = \sum_{k} \frac{\partial E_i}{\partial a_k} \frac{\partial a_k}{\partial a_j} = h^\prime(a_j) \sum_{k} w_{kj} \delta_k \end{align*}
Note that the recursion starts from the output and goes through the network backward.
Evaluate the required derivatives
\begin{align*} \frac{\partial E_i}{\partial w_{ji}} = \frac{\partial E_i}{\partial a_{j}} \frac{\partial a_j}{\partial w_{ji}} = \delta_j z_i \end{align*}
The technique of backpropagation can also be applied to the calculation of Jacobian and Hessian matrix where
\begin{align*} J_{ki} \equiv \frac{\partial y_k}{\partial x_i}, \text{ and } \mathbf{H} \sim \frac{\partial^2 E}{\partial w_{ji} \partial w_{lk}} \end{align*}
We consider a simple task: learning the XOR function to demonstrate the training process.
The XOR function (“exclusive or”) is an operation on two binary values such that
\begin{align*} f(x_1, x_2) = \left\{ \begin{aligned} &0 && \text{ if } x_1 = x_2 \\ &1 && \text{ otherwise.} \end{aligned} \right. \end{align*}
[13]:
from sklearn.linear_model import LinearRegression
x_train = np.array([[0, 0],[0, 1],[1, 0],[1, 1]])
t_train = np.array([0, 1, 1, 0])
x0, x1 = np.meshgrid(np.linspace(0, 1, 100), np.linspace(0, 1, 100))
x_test = np.array([x0, x1]).reshape(2, -1).T
t = LinearRegression().fit(x_train, t_train).predict(x_test)
plt.figure(figsize=(5, 4))
plt.scatter(x_train[:, 0], x_train[:, 1], c=t_train)
levels = np.linspace(0, 1, 5)
plt.contourf(x0, x1, np.asarray(t).reshape(100, 100), levels, alpha=0.2)
plt.colorbar()
plt.show()
toggle()
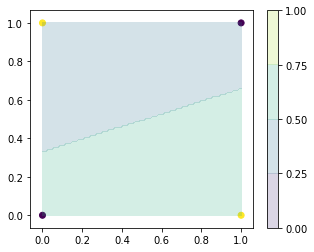
[13]:
The dots indicate the target values of inputs. It is clear that linear function cannot describe the feature, because any hyperplane will have both target values 0 and 1 on one-side. This is demonstrated by a linear regression model.
We provide details on learning the XOR function by using a simple neural network.
We have
input
\begin{align} \mathbf{x} = \left( \begin{array}{l} 0 \\ 0 \\ 1 \\ \end{array} \right) \text{ or } \left( \begin{array}{l} 0 \\ 1 \\ 1 \\ \end{array} \right) \text{ or } \left( \begin{array}{l} 1 \\ 0 \\ 1 \\ \end{array} \right) \text{ or } \left( \begin{array}{l} 1 \\ 1 \\ 1 \\ \end{array} \right) \nonumber \end{align}
hidden layer
\begin{align} a^1_{j} = {\mathbf{w}^1_j}^T \mathbf{x} \text{, } \mathbf{a}^1 = (a^1_{j} :\forall j)^T \text{ and } z_{j} = h(a^1_{j}) \text{, } \mathbf{z} = (z_{j}: \forall j)^T \nonumber \end{align}
output
\begin{align} a^2_{k} = {\mathbf{w}^2_{k}}^T \mathbf{z} \text{ and } y = y_k = h(a^2_{k}) \nonumber \end{align}
Note that, in this case, \(k = \{1\}\).
Feed-Forward
To apply stochastic gradient decent, we consider one instance and its error function
\begin{align} E_i = \frac{1}{2} \left( y - t \right)^2 \nonumber \end{align}
\begin{align} \mathbf{z} = h\left({\mathbf{W}^1}^T \mathbf{x} \right) \text{ and } y = h\left({\mathbf{w}^2}^T \mathbf{z}\right) \nonumber \end{align}
where
\begin{align} \mathbf{W}^{1} = (\mathbf{w}^1_{j} : \forall j) \nonumber \end{align}
Derivatives
Let \(h = \tanh\).
\begin{align} \sigma^\prime(x) &= \sigma(x) (1- \sigma(x)) \nonumber\\ \tanh^\prime(x) &= 1 -\tanh^2(x) \nonumber \end{align}
Error Backpropagation
\begin{align} \delta^2_{k} &\equiv \frac{\partial E_i}{\partial a^2_k} = \frac{\partial E_i}{\partial y} \frac{\partial y}{\partial a^2_k} = (y-t) h^\prime(a^2_k) = (y-t) (1- h^2(a^2_k)) = (y-t) (1- y^2) \nonumber \\ \delta^1_{j} &\equiv \frac{\partial E_i}{\partial a^1_{j}} = \sum_k \frac{\partial E_i}{\partial a^2_{k}} \frac{\partial a^2_{k}}{\partial z_j} \frac{\partial z_j}{\partial a^1_{j}} = h^\prime(a^1_{j}) \sum_{k} \delta^2_{k} w^2_{k,j} = (1-z_j^2) \sum_{k} \delta^2_{k} w^2_{k,j} \nonumber \end{align}
\begin{align} \frac{\partial E_i}{\partial \mathbf{w}^2_k} & = \frac{\partial E_i}{\partial a^2_k} \frac{\partial a^2_k}{\partial \mathbf{w}^2_k} = \delta^2_{k} \mathbf{z} \nonumber \\ \frac{\partial E_i}{\partial \mathbf{w}^1_j} & = \frac{\partial E_i}{\partial a^1_j} \frac{\partial a^1_j}{\partial \mathbf{w}^1_j} = \delta^1_{j} \mathbf{x} \nonumber \end{align}
The code realize the neural network and backpropagation algorithm. The plot shows that the XOR function is correctly learned by our neural network.
[14]:
def sigmoid(x):
return 1.0/(1.0 + np.exp(-x))
def sigmoid_prime(x):
return x*(1.0-x)
def tanh(x):
return np.tanh(x)
def tanh_prime(x):
return 1.0 - x**2
class NeuralNetwork:
def __init__(self, layers, activation='tanh'):
if activation == 'sigmoid':
self.activation = sigmoid
self.activation_prime = sigmoid_prime
elif activation == 'tanh':
self.activation = tanh
self.activation_prime = tanh_prime
# Set weights
self.weights = []
# layers = [2,2,1]
# range of weight values (-1,1)
# input and hidden layers - random((2+1, 2+1)) : 3 x 3
for i in range(1, len(layers) - 1):
r = 2*np.random.random((layers[i-1] + 1, layers[i] + 1)) -1
self.weights.append(r)
# output layer - random((2+1, 1)) : 3 x 1
r = 2*np.random.random( (layers[i] + 1, layers[i+1])) - 1
self.weights.append(r)
def fit(self, X, t, learning_rate=0.2, epochs=100000):
ones = np.atleast_2d(np.ones(X.shape[0]))
X = np.concatenate((ones.T, X), axis=1)
# Add the bias unit to the input layer X, so that
# X = [[1. 0. 0.]
# [1. 0. 1.]
# [1. 1. 0.]
# [1. 1. 1.]]
for k in range(epochs):
i = np.random.randint(X.shape[0])
z = [X[i]]
for l in range(len(self.weights)):
z.append(self.activation(np.array(self.weights[l]).T @ np.array(z[l])))
# backpropagation
# output layer y = z[-1]
error = z[-1] - t[i]
deltas = [error * self.activation_prime(z[-1])]
for l in range(len(self.weights) - 1, 0, -1):
deltas.append(np.dot(self.weights[l], deltas[-1]) * self.activation_prime(z[l]))
deltas.reverse()
for i in range(len(self.weights)):
self.weights[i] -= learning_rate * np.array(z[i])[:,None].dot(np.array(deltas[i])[:,None].T)
if k % 10000 == 0: print('epochs:{}, error={}'.format(k, error))
def predict(self, X):
ones = np.atleast_2d(np.ones(X.shape[0]))
y = np.concatenate((ones.T, X), axis=1)
for l in range(0, len(self.weights)):
y = self.activation(np.dot(y, self.weights[l]))
return y
toggle()
[14]:
[15]:
nn = NeuralNetwork([2,2,1], activation='tanh')
nn.fit(x_train, t_train)
np.set_printoptions(suppress=True)
# print(np.append(x_train, nn.predict(x_train), axis=1))
plt.figure(figsize=(5, 4))
plt.scatter(x_train[:, 0], x_train[:, 1], c=t_train)
x0, x1 = np.meshgrid(np.linspace(0, 1, 100), np.linspace(0, 1, 100))
x_test = np.array([x0, x1]).reshape(2, -1).T
levels = np.linspace(0, 1, 5)
plt.contourf(x0, x1, np.asarray(nn.predict(x_test)).reshape(100, 100), levels, alpha=0.2)
plt.colorbar()
plt.show()
epochs:0, error=[-0.07482236]
epochs:10000, error=[0.00031893]
epochs:20000, error=[0.00029467]
epochs:30000, error=[-0.00716532]
epochs:40000, error=[-0.00477388]
epochs:50000, error=[-0.00421749]
epochs:60000, error=[-1.54676533e-07]
epochs:70000, error=[2.76519559e-05]
epochs:80000, error=[4.02423604e-05]
epochs:90000, error=[-0.00302211]

Regression¶
We are attempting to predict the median price of homes in a given Boston suburb in the mid-1970s, given a few data points about the suburb at the time, such as the crime rate, the local property tax rate, etc.
The dataset has very few data points, only 506 in total, split between 404 training samples and 102 test samples, and each “feature” in the input data (e.g. the crime rate is a feature) has a different scale. For instance some values are proportions, which take a values between 0 and 1, others take values between 1 and 12, others between 0 and 100.
[16]:
from keras.datasets import boston_housing
(train_data, train_targets), (test_data, test_targets) = boston_housing.load_data()
[17]:
train_data.shape, test_data.shape, train_targets[:10]
[17]:
((404, 13),
(102, 13),
array([15.2, 42.3, 50. , 21.1, 17.7, 18.5, 11.3, 15.6, 15.6, 14.4]))
The data comprises 13 features as follows:
Per capita crime rate.
Proportion of residential land zoned for lots over 25,000 square feet.
Proportion of non-retail business acres per town.
Charles River dummy variable (= 1 if tract bounds river; 0 otherwise).
Nitric oxides concentration (parts per 10 million).
Average number of rooms per dwelling.
Proportion of owner-occupied units built prior to 1940.
Weighted distances to five Boston employment centres.
Index of accessibility to radial highways.
Full-value property-tax rate per $10,000.
Pupil-teacher ratio by town.
\(1000 \times (B_k - 0.63)^2\) where \(B_k\) is the proportion of Black people by town.
% lower status of the population.
The targets are the median values of owner-occupied homes, in thousands of dollars. The prices are typically between $10,000 and $50,000.
Preparing the data¶
It would be problematic to feed into a neural network values that all take wildly different ranges. The network might be able to automatically adapt to such heterogeneous data, but it would definitely make learning more difficult. A widespread best practice to deal with such data is to do feature-wise normalization: for each feature in the input data (a column in the input data matrix), we will subtract the mean of the feature and divide by the standard deviation, so that the feature will be centered around 0 and will have a unit standard deviation.
[18]:
mean = train_data.mean(axis=0)
train_data -= mean
std = train_data.std(axis=0)
train_data /= std
test_data -= mean
test_data /= std
Note that the quantities that we use for normalizing the test data have been computed using the training data. We should never use in our workflow any quantity computed on the test data, even for something as simple as data normalization.
Building the network¶
When little training data is available, it’s preferable to use a small network with few hidden layers (typically only one or two), in order to avoid severe overfitting.
[19]:
def build_model():
model = models.Sequential()
model.add(layers.Dense(64, activation='relu',
input_shape=(train_data.shape[1],)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(1))
model.compile(optimizer='rmsprop', loss='mse', metrics=['mae'])
return model
The network ends with a single unit, and no activation (i.e. it will be linear layer). This is a typical setup for scalar regression (i.e. regression where we are trying to predict a single continuous value).
We compile the network with the mse loss function – Mean Squared Error and monitor a new metric during training: mae – Mean Absolute Error.
K-fold Validation¶
To evaluate our network while we keep adjusting its parameters (such as the number of epochs used for training), we could simply split the data into a training set and a validation set. However, because we have so few data points, the validation set would end up being very small (e.g. about 100 examples). A consequence is that our validation scores may change a lot depending on which data points we choose to use for validation and which we choose for training, i.e. the validation scores may have a high variance with regard to the validation split. This would prevent us from reliably evaluating our model.
The best practice in such situations is to use K-fold cross-validation. It consists of splitting the available data into K partitions (typically K=4 or 5), then instantiating K identical models, and training each one on K-1 partitions while evaluating on the remaining partition. The validation score for the model used would then be the average of the K validation scores obtained.
Let’s train the network for 300 epochs. To keep a record of how well the model did at each epoch, we save the per-epoch validation score log.
[20]:
def k_fold_validate():
k = 4
num_val_samples = len(train_data) // k
num_epochs = 300
all_scores = []
all_mae_histories = []
for i in range(k):
print('processing fold #', i)
# Prepare the validation data: data from partition # k
val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]
val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]
# Prepare the training data: data from all other partitions
partial_train_data = np.concatenate(
[train_data[:i * num_val_samples],
train_data[(i + 1) * num_val_samples:]],
axis=0)
partial_train_targets = np.concatenate(
[train_targets[:i * num_val_samples],
train_targets[(i + 1) * num_val_samples:]],
axis=0)
model = build_model()
# Train the model (in silent mode, verbose=0)
history = model.fit(partial_train_data, partial_train_targets,
validation_data=(val_data, val_targets),
epochs=num_epochs, batch_size=1, verbose=0)
# Evaluate the model on the validation data
val_mse, val_mae = model.evaluate(val_data, val_targets, verbose=0)
all_scores.append(val_mae)
mae_history = history.history['val_mean_absolute_error']
all_mae_histories.append(mae_history)
df = pd.DataFrame(data=np.array(all_mae_histories).T, columns=['mae0', 'mae1', 'mae2', 'mae3'])
df.to_csv(base_dir+'\\house.csv', header=True, index=False)
toggle()
[20]:
[21]:
df = pd.read_csv(base_dir+'\\house_scores.csv')
df.score, np.mean(df.score)
[21]:
(0 2.410330
1 3.169268
2 2.872851
3 2.974952
Name: score, dtype: float64, 2.856850517268228)
As you can notice, the different runs show rather different validation scores. Their average is a much more reliable metric than any single of these scores.
We can compute the average of the per-epoch MAE scores for all folds. We also plot an exponential moving average of the average MAE curve to better demonstrate the overfitting.
[22]:
df = pd.read_csv(base_dir+'\\house.csv')
average_mae_history = np.mean(df, axis=1)
# exponential smoothing a curve
def smooth_curve(points, factor=0.9):
smoothed_points = []
for point in points:
if smoothed_points:
previous = smoothed_points[-1]
smoothed_points.append(previous * factor + point * (1 - factor))
else:
smoothed_points.append(point)
return smoothed_points
smooth_mae_history = smooth_curve(average_mae_history)
fig = plt.figure(figsize=(10,5))
plt.plot(range(1, len(average_mae_history) + 1), average_mae_history, label='MAE')
plt.plot(range(1, len(smooth_mae_history) + 1), smooth_mae_history, label='Smoothed MAE')
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.ylim(2.2, 3.2)
plt.title('Average MAE')
plt.legend()
plt.show()
toggle()
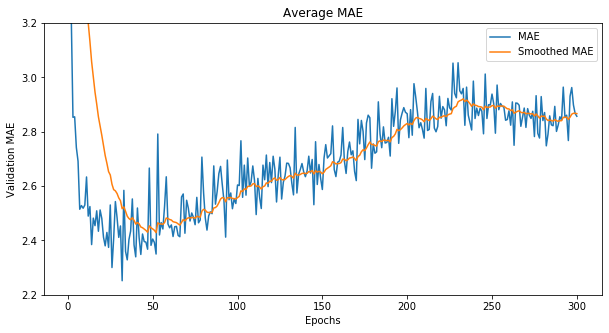
[22]:
It seems that validation MAE stops improving significantly after 50-60 epochs. Past that point, we start overfitting.
[23]:
model = build_model()
# Train it on the entirety of the data.
model.fit(train_data, train_targets, epochs=50, batch_size=16, verbose=0)
test_mse_score, test_mae_score = model.evaluate(test_data, test_targets)
K.clear_session()
del model
test_mae_score
102/102 [==============================] - 0s 3ms/step
[23]:
2.7497070256401512
Our predictions on the testing data are still off by more than $2,700.
Classification¶
We consider movie-review binary classification problem with positive or negative reviews based on IMDB dataset and a multi-class classification problem on Reuters dataset.
IMDB dataset¶
IMDB dataset is a set of 50,000 highly-polarized reviews from the Internet Movie Database. They are split into 25,000 reviews for training and 25,000 reviews for testing, each set consisting in 50% negative and 50% positive reviews.
The argument num_words=10000 restricts the data to the 10,000 most frequently occurring words found in the data.
[24]:
# Revise np.load because of keras error msg "Object arrays cannot be loaded when allow_pickle=False"
np_load_old = np.load
# modify the default parameters of np.load
np.load = lambda *a,**k: np_load_old(*a, allow_pickle=True, **k)
# call load_data with allow_pickle implicitly set to true
from keras.datasets import imdb
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)
# restore np.load for future normal usage
np.load = np_load_old
toggle()
[24]:
Training data is stored as numberic array. For example,
[25]:
train_data[0][:10]
[25]:
[1, 14, 22, 16, 43, 530, 973, 1622, 1385, 65]
Therefore, we need a dictionary mapping words to an interger index:
word_index = imdb.get_word_index()
Then we reverse it to have a dictionary mapping integer indices to words
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])
At last, we can decode the review (note that our indices were offset by 3 because 0, 1 and 2 are reserved indices for “padding”, “start of sequence”, and “unknown”).
For example, we can deconde the first 10 words as follows.
[26]:
word_index = imdb.get_word_index()
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])
print("Deconde review train_data[0][:10]]:\n",
' '.join([reverse_word_index.get(i - 3, '?') for i in train_data[0][:10]]))
display('Example of dictionary:\n',dict(sorted(reverse_word_index.items())[10:20]))
Deconde review train_data[0][:10]]:
? this film was just brilliant casting location scenery story
'Example of dictionary:\n'
{11: 'this',
12: 'that',
13: 'was',
14: 'as',
15: 'for',
16: 'with',
17: 'movie',
18: 'but',
19: 'film',
20: 'on'}
[27]:
def show_review(index):
decoded_review = ' '.join([reverse_word_index.get(i - 3, '?') for i in train_data[index]])
print('Review:\n', decoded_review)
print('Number of words:', len(decoded_review.split()))
print('Indices for all ?s:', [train_data[index][i] for i, w in enumerate(decoded_review.split()) if w == '?'])
style = {'description_width': 'initial'}
interact(show_review, index=widgets.IntSlider(min=0,max=30,step=1,value=10,description='Index of Review:',style=style));
Preparing the data¶
We cannot feed lists of integers into a neural network. We have to turn our lists into tensors. There are two ways we could do that:
We could pad our lists so that they all have the same length, and turn them into an integer tensor of shape (samples, word_indices), then use as first layer in our network a layer capable of handling such integer tensors (the Embedding layer, which we will cover later).
We could one-hot-encode our lists to turn them into vectors of 0s and 1s. Concretely, this would mean for instance turning the sequence [3, 5] into a 10,000-dimensional vector that would be all-zeros except for indices 3 and 5, which would be ones. Then we could use as first layer in our network a Dense layer, capable of handling floating point vector data.
We will go with the latter solution. Let’s vectorize our data manually for maximum clarity. An example for vectorize array
[28]:
def vectorize_sequences(sequences, dimension=10000):
# Create an all-zero matrix of shape (len(sequences), dimension)
results = np.zeros((len(sequences), dimension))
for i, sequence in enumerate(sequences):
results[i, sequence] = 1. # set specific indices of results[i] to 1s
return results
vectorize_sequences([[1,2,5],[3,5]], dimension=10)
[28]:
array([[0., 1., 1., 0., 0., 1., 0., 0., 0., 0.],
[0., 0., 0., 1., 0., 1., 0., 0., 0., 0.]])
[29]:
x_train = vectorize_sequences(train_data)
x_test = vectorize_sequences(test_data)
y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')
So far, Our input data is simply vectors with values 0 or 1, and our labels are scalars (1s and 0s). The easiest setup you will ever encounter. Fully connected (Dense) layers with relu activation typically performs well on such a dataset.
Building the network¶
Our network architecture includes:
Two intermediate layers with 16 hidden units each, and
a third layer which will output the scalar prediction regarding the sentiment of the current review.
The intermediate layers will use relu as their “activation function”, and the final layer will use a sigmoid activation so as to output a probability (a score between 0 and 1, indicating how likely the sample is to have the target “1”, i.e. how likely the review is to be positive).
Hidden unit is a single dimension in the representation space of the layer. Each Dense layer with a relu activation implements the following chain of tensor operations:
\begin{align*} \text{output = relu (dot($W$, input) + $b$)} \end{align*}
Having 16 hidden units means that the weight matrix W will have shape (input_dimension, 16), i.e. the dot product with W will project the input data onto a 16-dimensional representation space.
Intuitively, the dimensionality of your representation space is how much freedom you are allowing the network to have when learning internal representations.
Having more hidden units (a higher-dimensional representation space) allows your network to learn more complex representations, but it
makes your network more computationally expensive and
may lead to overfitting
The rmsprop optimizer is generally a good enough choice of optimizer whatever your problem.
Since we are facing a binary classification problem, we end our network with a single-unit layer with a sigmoid activation. It is better to use the binary_crossentropy loss, although you have other viable choices, for instance, you could use loss function: mean_squared_error. But crossentropy is usually the best choice when you are dealing with models that output probabilities.
If we want to configure the parameters of optimizer, or pass a custom loss function or metric function. This can be done by passing an optimizer class instance as the optimizer argument or passing function objects as the loss or metrics arguments:
from keras import optimizers
from keras import losses
from keras import metrics
model.compile(optimizer=optimizers.RMSprop(lr=0.001),
loss=losses.binary_crossentropy,
metrics=[metrics.binary_accuracy])
In order to monitor during training the accuracy of the model on data that it has never seen before, we will create a validation set by setting apart 10,000 samples from the original training data.
[30]:
def train_imdb_1():
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['accuracy'])
x_val = x_train[:10000]
partial_x_train = x_train[10000:]
y_val = y_train[:10000]
partial_y_train = y_train[10000:]
history = model.fit(partial_x_train, partial_y_train, epochs=20, batch_size=512,
validation_data=(x_val, y_val), verbose=0);
model.save(base_dir+"\\imdb_1.h5")
df = pd.DataFrame.from_dict(data=history.history, orient='columns')
df.to_csv(base_dir+'\\history_imdb.csv', header=True, index=False)
K.clear_session()
del model
toggle()
[30]:
[31]:
model = models.load_model(base_dir+"\\imdb_1.h5")
results = model.evaluate(x_test, y_test)
print('model achieves an accuracy of {}% for testing data'.format(round(results[1]*100,2)))
25000/25000 [==============================] - 4s 150us/step
model achieves an accuracy of 85.36% for testing data
Validating the Approach¶
model.fit() returns a history object. This object has a member history, which is a dictionary containing data about everything that happened during training. The dictionary has 4 keys “val_loss”, “val_acc”, “loss”, “acc” which are loss/accuracy percentages for validation and training datasets. We plot the training and validation loss, as well as the training and validation accuracy
[32]:
df = pd.read_csv(base_dir+'\\history_imdb.csv')
history = df.to_dict()
acc = list(history['acc'].values())
val_acc = list(history['val_acc'].values())
loss = list(history['loss'].values())
val_loss = list(history['val_loss'].values())
epochs = range(len(acc))
fig = plt.figure(figsize=(18,5))
plt.subplot(1, 2, 1)
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'r', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'r', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
toggle()
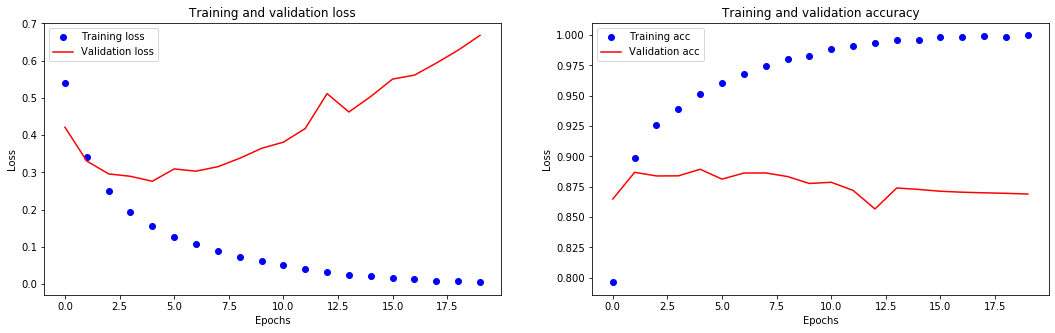
[32]:
The training loss decreases with every epoch and the training accuracy increases with every epoch. That’s what you would expect when running gradient descent optimization – the quantity you are trying to minimize should get lower with every iteration.
However, this isn’t the case for the validation loss and accuracy: they seem to peak at the fourth epoch.
Overfitting: a model that performs better on the training data isn’t necessarily a model that will do better on data it has never seen before. We ended up learning representations that are specific to the training data and do not generalize to data outside of the training set.
In this case, to prevent overfitting, we could simply stop training after 4 epochs.
[33]:
def train_imdb_2():
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['accuracy'])
model.fit(x_train, y_train, epochs=4, batch_size=512, verbose=0)
model.save(base_dir+"\\imdb_2.h5")
K.clear_session()
del model
toggle()
[33]:
[34]:
model = models.load_model(base_dir+"\\imdb_2.h5")
results = model.evaluate(x_test, y_test)
print('\n model achieves an accuracy of {}% for testing data'.format(round(results[1]*100,2)))
25000/25000 [==============================] - 4s 143us/step
model achieves an accuracy of 88.32% for testing data
Prediction¶
After having trained a network, we can generate the likelihood of reviews being positive by using the predict method
[35]:
model.predict(x_test)
[35]:
array([[0.19963935],
[0.9995559 ],
[0.8614843 ],
...,
[0.09901541],
[0.07926401],
[0.50504327]], dtype=float32)
There are some Further experiments can be tried:
We were using 2 hidden layers. Try to use 1 or 3 hidden layers and see how it affects validation and test accuracy.
Try to use layers with more hidden units or less hidden units: 32 units, 64 units…
Try to use the mse loss function instead of binary_crossentropy.
Try to use the tanh activation (an activation that was popular in the early days of neural networks) instead of relu.
Reuters Dataset¶
For IMDB dataset, we classify vector inputs into two mutually exclusive classes using a densely-connected neural network. In this section, we will build a network to classify Reuters newswires into 46 different mutually-exclusive topics. Since we have many classes, this problem is an instance of multi-class classification.
Reuters dataset, a set of short newswires and their topics, published by Reuters in 1986. It’s a very simple, widely used toy dataset for text classification. There are 46 different topics; some topics are more represented than others, but each topic has at least 10 examples in the training set.
We have 8,982 training examples and 2,246 test examples. As with the IMDB reviews, each example is a list of integers (word indices).
[36]:
np_load_old = np.load
np.load = lambda *a,**k: np_load_old(*a, allow_pickle=True, **k)
from keras.datasets import reuters
from keras.utils.np_utils import to_categorical
(train_data, train_labels), (test_data, test_labels) = reuters.load_data(num_words=10000)
np.load = np_load_old
x_train = vectorize_sequences(train_data)
x_test = vectorize_sequences(test_data)
y_train = to_categorical(train_labels)
y_test = to_categorical(test_labels)
# we set apart 1000 samples in the training data as validation set
partial_x_train = x_train[1000:]
x_val = x_train[:1000]
partial_y_train = y_train[1000:]
y_val = y_train[:1000]
toggle()
[36]:
Similar to the IMDB dataset, we prepare the data by vectorizing the data with the exact same code, building the network and validating the approach.
However, there is a new constraint that changes our network architecture: the number of output classes has gone from 2 to 46, i.e. the dimensionality of the output space is much larger.
In a stack of Dense layers, each layer can only access information present in the output of the previous layer. If one layer drops some information relevant to the classification problem, this information can never be recovered by later layers.
Therefore, we cannot use 16-dimensional intermediate layers as for IMDB dataset, because a 16-dimensional space may be too limited to learn to separate 46 different classes. Such small layers may act as information bottlenecks, permanently dropping relevant information. For this reason we will use larger layers with 64 units.
We can see what happens when we introduce an information bottleneck by having intermediate layers significantly less than 46-dimensional, e.g. 4-dimensional by changing the code
model.add(layers.Dense(64, activation='relu'))
to
model.add(layers.Dense(4, activation='relu'))
The last layer uses a softmax activation. It means that the network will output a probability distribution over the 46 different output classes, i.e. for every input sample, the network will produce a 46-dimensional output vector where
output[i]is the probability that the sample belongs to class i. The 46 scores will sum to 1.The best loss function to use in this case is categorical_crossentropy.
[37]:
def train_reuters_1():
model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))
model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy'])
history = model.fit(partial_x_train, partial_y_train, epochs=20, batch_size=512,
validation_data=(x_val, y_val), verbose=0)
model.save(base_dir+"\\reuters_1.h5")
df = pd.DataFrame.from_dict(data=history.history, orient='columns')
df.to_csv(base_dir+'\\history_reuters1.csv', header=True, index=False)
K.clear_session()
del model
toggle()
[37]:
[38]:
model = models.load_model(base_dir+"\\reuters_1.h5")
results = model.evaluate(x_test, y_test)
print('model achieves an accuracy of {}% for testing data'.format(round(results[1]*100,2)))
2246/2246 [==============================] - 0s 197us/step
model achieves an accuracy of 77.83% for testing data
[39]:
df = pd.read_csv(base_dir+'\\history_reuters1.csv')
history = df.to_dict()
acc = list(history['acc'].values())
val_acc = list(history['val_acc'].values())
loss = list(history['loss'].values())
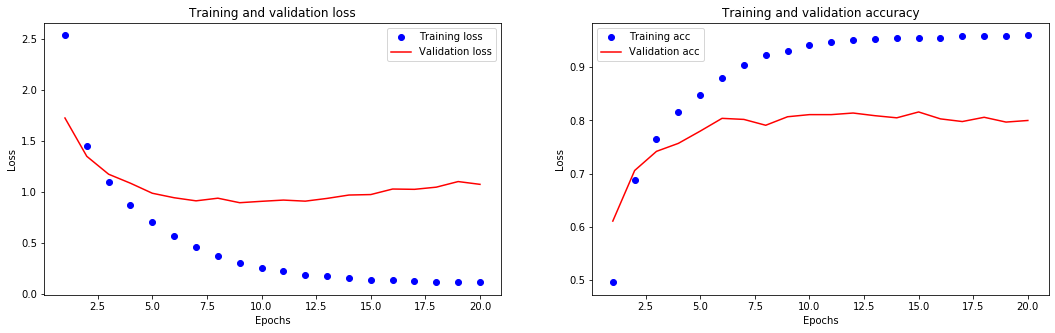
val_loss = list(history['val_loss'].values())
epochs = range(1, len(acc)+1)
fig = plt.figure(figsize=(18,5))
plt.subplot(1, 2, 1)
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'r', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'r', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
toggle()
[39]:
It seems that the network starts overfitting after 9 epochs. Let’s train a new network from scratch for 6 epochs, then evaluate it on the test set.
[40]:
def train_reuters_2():
model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))
model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy'])
history = model.fit(partial_x_train, partial_y_train, epochs=9, batch_size=512,
validation_data=(x_val, y_val), verbose=0)
model.save(base_dir+"\\reuters_2.h5")
K.clear_session()
del model
toggle()
[40]:
[41]:
model = models.load_model(base_dir+"\\reuters_2.h5")
results = model.evaluate(x_test, y_test)
print('model achieves an accuracy of {}% for testing data'.format(round(results[1]*100,2)))
2246/2246 [==============================] - 0s 188us/step
model achieves an accuracy of 78.63% for testing data
Prediction: model.predict() returns a probability distribution over all 46 topics. We need to use np.argmax(predictions,axis=1) to find out predicted class, which is the class with the highest probability.
[42]:
predictions = model.predict(x_test)
display(predictions.shape)
predictions.shape
predictions = np.argmax(predictions,axis=1)
predictions
(2246, 46)
[42]:
array([ 3, 10, 1, ..., 3, 3, 1], dtype=int64)
Regularization¶
The fundamental issue in machine learning is the tension between optimization and generalization.
“Optimization” refers to the process of adjusting a model to get the best performance possible on the training data (the “learning” in “machine learning”), while “generalization” refers to how well the trained model would perform on data it has never seen before.
The goal of the game is to get good generalization, of course, but we do not control generalization; we can only adjust the model based on its training data.
Size of the Network¶
The number of hidden units in each layer is a free parameter that can be adjusted to have the best predictive performance. Deep learning models tend to be good at fitting to the training data, but the real challenge is generalization, not fitting.
In deep learning, the number of learnable parameters in a model is often referred to as the model’s “capacity”. There is a compromise to be found between “too much capacity” and “not enough capacity”.
[43]:
def create_data(n=10):
np.random.seed(11111113)
x = np.linspace(0, 1, n)[:, None]
return x, np.sin(2 * np.pi * x) + np.random.normal(scale=0.25, size=(10, 1))
def regularization():
x_train, y_train = create_data()
for i, m in enumerate([1, 3, 30]):
model = models.Sequential()
model.add(layers.Dense(m, activation='tanh', input_shape=(1,)))
model.add(layers.Dense(1))
model.compile(optimizer='Adam',loss='mean_squared_error', metrics=['mae'])
model.fit(x_train, y_train, epochs=10000, batch_size=1, verbose=0);
model.save(base_dir+"\\regularization_{}.h5".format(m))
K.clear_session()
del model
toggle()
[43]:
[44]:
x_train, y_train = create_data()
x = np.linspace(0, 1, 100)[:, None]
plt.figure(figsize=(20, 5))
for i, m in enumerate([1,3,30]):
plt.subplot(1, 3, i + 1)
model = models.load_model(base_dir+"\\regularization_{}.h5".format(m))
y = model.predict(x)
plt.scatter(x_train, y_train, marker="x", color="r")
plt.plot(x, np.sin(2 * np.pi * x), color='y')
plt.plot(x, y, color="k")
plt.title("# hidden units={}".format(m))
plt.show()
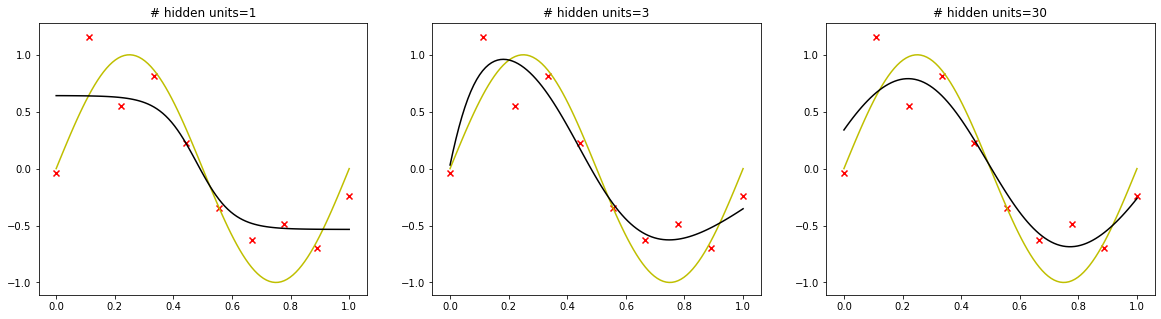
We consider the movie-review classification problem.
[45]:
def network_size():
np_load_old = np.load
np.load = lambda *a,**k: np_load_old(*a, allow_pickle=True, **k)
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)
np.load = np_load_old
x_train = vectorize_sequences(train_data)
x_test = vectorize_sequences(test_data)
y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')
original_model = models.Sequential()
original_model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
original_model.add(layers.Dense(16, activation='relu'))
original_model.add(layers.Dense(1, activation='sigmoid'))
original_model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc'])
original_hist = original_model.fit(x_train, y_train, epochs=20, batch_size=512,
validation_data=(x_test, y_test), verbose=0)
df = pd.DataFrame.from_dict(data=original_hist.history, orient='columns')
df.to_csv(base_dir+'\\history_imdb_orig.csv', header=True, index=False)
K.clear_session()
del original_model
smaller_model = models.Sequential()
smaller_model.add(layers.Dense(4, activation='relu', input_shape=(10000,)))
smaller_model.add(layers.Dense(4, activation='relu'))
smaller_model.add(layers.Dense(1, activation='sigmoid'))
smaller_model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc'])
smaller_model_hist = smaller_model.fit(x_train, y_train, epochs=20, batch_size=512,
validation_data=(x_test, y_test), verbose=0)
df = pd.DataFrame.from_dict(data=smaller_model_hist.history, orient='columns')
df.to_csv(base_dir+'\\history_imdb_small.csv', header=True, index=False)
K.clear_session()
del smaller_model
bigger_model = models.Sequential()
bigger_model.add(layers.Dense(512, activation='relu', input_shape=(10000,)))
bigger_model.add(layers.Dense(512, activation='relu'))
bigger_model.add(layers.Dense(1, activation='sigmoid'))
bigger_model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc'])
bigger_model_hist = bigger_model.fit(x_train, y_train, epochs=20, batch_size=512,
validation_data=(x_test, y_test), verbose=0)
df = pd.DataFrame.from_dict(data=bigger_model_hist.history, orient='columns')
df.to_csv(base_dir+'\\history_imdb_big.csv', header=True, index=False)
K.clear_session()
del bigger_model
toggle()
[45]:
[46]:
df = pd.read_csv(base_dir+'\\history_imdb_orig.csv')
history = df.to_dict()
original_val_loss = list(history['val_loss'].values())
df = pd.read_csv(base_dir+'\\history_imdb_small.csv')
history = df.to_dict()
smaller_model_val_loss = list(history['val_loss'].values())
df = pd.read_csv(base_dir+'\\history_imdb_big.csv')
history = df.to_dict()
bigger_model_val_loss = list(history['val_loss'].values())
epochs = range(1, len(original_val_loss)+1)
fig = plt.figure(figsize=(18,5))
plt.subplot(1, 2, 1)
plt.plot(epochs, original_val_loss, 'r', label='Original model')
plt.plot(epochs, smaller_model_val_loss, 'bo', label='Smaller model')
plt.xlabel('Epochs')
plt.ylabel('Validation loss')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(epochs, original_val_loss, 'r', label='Original model')
plt.plot(epochs, bigger_model_val_loss, 'mo', label='Bigger model')
plt.xlabel('Epochs')
plt.ylabel('Validation loss')
plt.legend()
plt.show()
toggle()
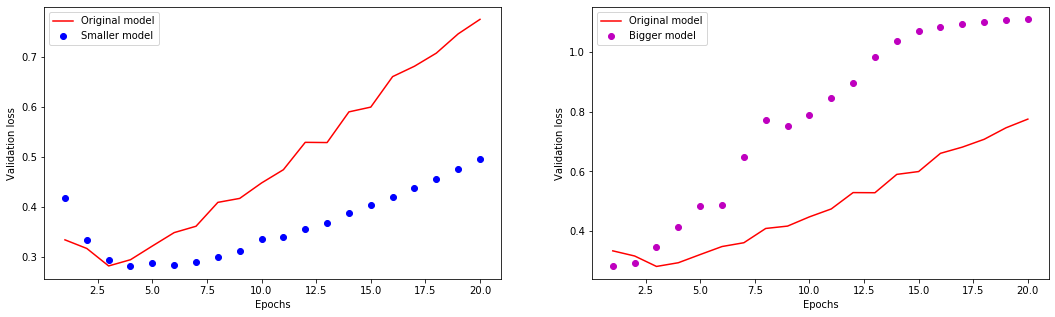
[46]:
Weight Regularization¶
A common way to mitigate overfitting is to put constraints on the complexity of a network by forcing its weights to only take small values. It is done by adding to the loss function of the network a cost associated with having large weights. This cost comes in two flavors:
L1 regularization, where the cost added is proportional to the absolute value of the weights coefficients.
L2 regularization, where the cost added is proportional to the square of the value of the weights coefficients. L2 regularization is also called weight decay in the context of neural networks.
We have shown that early stopping is an alternative to regularization, which can control the effective complexity of a network.
[47]:
def train_l2():
np_load_old = np.load
np.load = lambda *a,**k: np_load_old(*a, allow_pickle=True, **k)
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)
np.load = np_load_old
x_train = vectorize_sequences(train_data)
x_test = vectorize_sequences(test_data)
y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')
from keras import regularizers
l2_model = models.Sequential()
l2_model.add(layers.Dense(16, kernel_regularizer=regularizers.l2(0.001),
activation='relu', input_shape=(10000,)))
l2_model.add(layers.Dense(16, kernel_regularizer=regularizers.l2(0.001),
activation='relu'))
l2_model.add(layers.Dense(1, activation='sigmoid'))
l2_model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc'])
l2_model_hist = l2_model.fit(x_train, y_train, epochs=20, batch_size=512,
validation_data=(x_test, y_test), verbose=0)
df = pd.DataFrame.from_dict(data=l2_model_hist.history, orient='columns')
df.to_csv(base_dir+'\\history_imdb_l2.csv', header=True, index=False)
K.clear_session()
del l2_model
toggle()
[47]:
[48]:
df = pd.read_csv(base_dir+'\\history_imdb_orig.csv')
history = df.to_dict()
original_val_loss = list(history['val_loss'].values())
df = pd.read_csv(base_dir+'\\history_imdb_l2.csv')
history = df.to_dict()
l2_model_val_loss = list(history['val_loss'].values())
plt.plot(epochs, original_val_loss, 'r', label='Original model')
plt.plot(epochs, l2_model_val_loss, 'bo', label='L2-regularized model')
plt.xlabel('Epochs')
plt.ylabel('Validation loss')
plt.legend()
plt.show()
toggle()
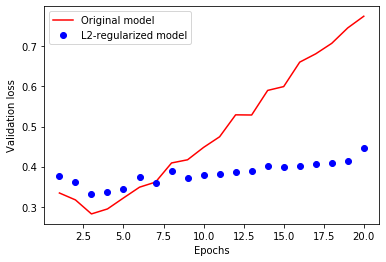
[48]:
Dropout¶
Dropout is one of the most effective and most commonly used regularization techniques for neural networks, developed by Hinton at the University of Toronto.
Dropout, applied to a layer, consists of randomly “dropping out” (i.e. setting to zero) a number of output features of the layer during training.
Let’s say a given layer would normally have returned a vector [0.2, 0.5, 1.3, 0.8, 1.1] for a given input sample during training; after applying dropout, this vector will have a few zero entries distributed at random, e.g. [0, 0.5, 1.3, 0, 1.1].
The “dropout rate” is the fraction of the features that are being zeroed-out; it is usually set between 0.2 and 0.5. At test time, no units are dropped out, and instead the layer’s output values are scaled down by a factor equal to the dropout rate, so as to balance for the fact that more units are active than at training time.
Consider a Numpy matrix containing the output of a layer, layer_output, of shape (batch_size, features). At training time, we would be zero-ing out at random a fraction of the values in the matrix:
This technique may seem strange and arbitrary. Why would this help reduce overfitting? Geoff Hinton has said that he was inspired, among other things, by a fraud prevention mechanism used by banks – in his own words: “I went to my bank. The tellers kept changing and I asked one of them why. He said he didn’t know but they got moved around a lot. I figured it must be because it would require cooperation between employees to successfully defraud the bank. This made me realize that randomly removing a different subset of neurons on each example would prevent conspiracies and thus reduce overfitting”.
The core idea is that introducing noise in the output values of a layer can break up happenstance patterns that are not significant (what Hinton refers to as “conspiracies”), which the network would start memorizing if no noise was present.
[49]:
def dropout():
np_load_old = np.load
np.load = lambda *a,**k: np_load_old(*a, allow_pickle=True, **k)
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)
np.load = np_load_old
x_train = vectorize_sequences(train_data)
x_test = vectorize_sequences(test_data)
y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')
dpt_model = models.Sequential()
dpt_model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
dpt_model.add(layers.Dropout(0.5))
dpt_model.add(layers.Dense(16, activation='relu'))
dpt_model.add(layers.Dropout(0.5))
dpt_model.add(layers.Dense(1, activation='sigmoid'))
dpt_model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc'])
dpt_model_hist = dpt_model.fit(x_train, y_train, epochs=20, batch_size=512,
validation_data=(x_test, y_test), verbose=0)
df = pd.DataFrame.from_dict(data=dpt_model_hist.history, orient='columns')
df.to_csv(base_dir+'\\history_imdb_dpt.csv', header=True, index=False)
K.clear_session()
del dpt_model
toggle()
[49]:
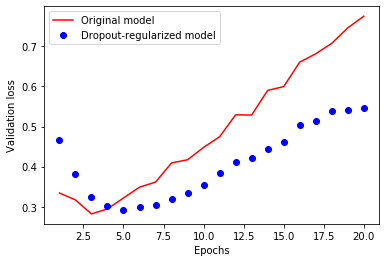
[50]:
df = pd.read_csv(base_dir+'\\history_imdb_orig.csv')
history = df.to_dict()
original_val_loss = list(history['val_loss'].values())
df = pd.read_csv(base_dir+'\\history_imdb_dpt.csv')
history = df.to_dict()
dpt_model_val_loss = list(history['val_loss'].values())
plt.plot(epochs, original_val_loss, 'r', label='Original model')
plt.plot(epochs, dpt_model_val_loss, 'bo', label='Dropout-regularized model')
plt.xlabel('Epochs')
plt.ylabel('Validation loss')
plt.legend()
plt.show()
toggle()
[50]: