[1]:
%run ../initscript.py
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
from scipy.stats import multivariate_normal
from ipywidgets import *
from IPython.display import display, HTML
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
import sys
sys.path.append('modules')
from DesignMat import Polynomial, Gaussian, Sigmoidal
from Regressor import LeastSquares, Bayesian, Empirical
data_path = "https://github.com/ming-zhao/Optimization-and-Learning/raw/master/data/"
def sinusoidal(x):
return np.sin(2 * np.pi * x)
def create_data(func, sample_size, std, domain=[0, 1]):
x = np.linspace(*domain, sample_size)
np.random.shuffle(x)
t = func(x) + np.random.normal(scale=std, size=x.shape)
return x, t
toggle()
[1]:
Linear Models for Regression¶
We define observation \(\mathbf{x} \equiv (x_{1},\ldots,x_{p})^\intercal\) with \(p\) attributes and target value \(y\). Given a training set \(\mathcal{D}\) with
\(n\) observations \(\mathbf{x}_i \equiv (x_{i1},\ldots,x_{ip})^\intercal\), \(\forall i \in N = \{1, \ldots, n\}\), and
target values \(\mathbf{y} \equiv (y_1,\ldots,y_n)^\intercal\)
We shall fit the data using a linear model
\begin{align} f(\mathbf{x}, \mathbf{w}) = w_0 + w_1 \phi_1(\mathbf{x}) + w_2 x_2 + \cdots + w_{m-1} \phi_{m-1}(\mathbf{x}) \nonumber \end{align}
where \(\phi_i\) is a transformation of \(\mathbf{x}\) called basis functions.
In the matrix form, we have
\begin{align*} f(\mathbf{x}, \mathbf{w}) &= \mathbf{\Phi} \mathbf{w} \\ \end{align*}
where
\begin{align*} \mathbf{w} &= (w_0, \ldots, w_{m-1}) \end{align*}
and
\begin{align*} \mathbf{\Phi} &= \left\{ \begin{array}{l} \phi(\mathbf{x}_1)\\ \phi(\mathbf{x}_2) \\ \vdots \\ \phi(\mathbf{x}_n) \end{array} \right\} = \left\{ \begin{array}{lllll} \phi_0(\mathbf{x}_1) = 1 & \phi_1(\mathbf{x}_1) & \phi_2(\mathbf{x}_1) & \ldots & \phi_{m-1}(\mathbf{x}_1) \\ \phi_0(\mathbf{x}_2) = 1& \phi_1(\mathbf{x}_2) & \phi_2(\mathbf{x}_2) & \ldots & \phi_{m-1}(\mathbf{x}_2) \\ \vdots & \vdots & \vdots & \ddots& \vdots\\ \phi_0(\mathbf{x}_n) = 1& \phi_1(\mathbf{x}_n) & \phi_2(\mathbf{x}_n) & \ldots & \phi_{m-1}(\mathbf{x}_n) \end{array} \right\}_{n \times m} \\ \end{align*}
When \(\phi_j(\mathbf{x}) = x_j\), we have linear regression with input matrix
\begin{align} \mathbf{\Phi} = \mathbf{X}_{n \times p} = (\mathbf{x}_1, \ldots, \mathbf{x}_n)^\intercal. \nonumber \end{align}
When \(p=1\) and \(\phi_j(x) = x^j\), we have polynomial fitting.
Note that the matrix \(\mathbf{X}\) should be of size \(n \times (p+1)\) because of regression constant. For the purpose of simplifying notations, we assume \(x_{i1} = 1\) \(\forall i \in N\) and hence ignore the notational inconvenience of dimension \(p+1\).
In a frequentist setting,
\(\mathbf{w}\) is considered to be a fixed parameter, whose value is determined by some form of “estimator”, and
error on this estimate are obtained by considering the distribution of possible observed data sets \(\mathcal{D}\).
In a Bayesian setting,
We assume a prior probability distribution \(p(\mathbf{w})\) before observing the data.
The effect of the observed data \(\mathcal{D}\) is expressed through \(p(\mathcal{D}|\mathbf{w})\), i.e., likelihood function.
Bayes’ theorem
\begin{align*} p(\mathbf{w}|\mathcal{D}) &= \frac{p(\mathcal{D}|\mathbf{w}) p(\mathbf{w})}{p(\mathcal{D})},\ \text{i.e., posterior} \propto \text{likelihood $\times$ prior} \end{align*}
evaluates the uncertainty in \(\mathbf{w}\) after \(\mathcal{D}\) is observed, where
\(p(\mathbf{w}|\mathcal{D})\) is the posterior probability after \(\mathcal{D}\) is observed,
\(p(\mathcal{D})\) is the probability of evidence.
Least Squares¶
We minimize residual sum of squares (RSS)
\begin{align*} \text{RSS}(\mathbf{w}) = \sum_{i=1}^{n} (y_i - f(\mathbf{x}_i, \mathbf{w}))^2 = (\mathbf{y} - \mathbf{\Phi} \mathbf{w})^\intercal(\mathbf{y} - \mathbf{\Phi}\mathbf{w}) \end{align*}
The first order condition gives
\begin{align*} \mathbf{\Phi}^\intercal (\mathbf{y} - \mathbf{\Phi}\mathbf{w}) = 0 \end{align*}
and the normal equation
\begin{align*} \mathbf{w} = (\mathbf{\Phi}^\intercal\mathbf{\Phi})^{-1} \mathbf{\Phi}^\intercal \mathbf{y} = \mathbf{\Phi}^\dagger \mathbf{y} \end{align*}
where \(\mathbf{\Phi}^\dagger\) is the Moore-Penrose pseudo-inverse of the matrix \(\mathbf{\Phi}\).
[2]:
hide_comment()
[2]:
Suppose \(y_i\) are uncorrelated with constant variance \(\sigma^2\), and \(\mathbf{x}_i\) are fixed.
Theorem: \(E(\mathbf{\hat{w}}) = \mathbf{w}\) and \(\text{Var}(\mathbf{\hat{w}}) = (\mathbf{\Phi}^\intercal \mathbf{\Phi})^{-1} \sigma^2\).
Proof:
\(\mathbf{\hat{w}}\) is an unbiased estimate of \(\mathbf{w}\):
\begin{align*} \text{E}(\mathbf{\hat{w}}) & = \text{E}((\mathbf{\Phi}^\intercal \mathbf{\Phi})^{-1} \mathbf{\Phi}^\intercal \mathbf{y}) = \text{E}((\mathbf{\Phi}^\intercal \mathbf{\Phi})^{-1} \mathbf{\Phi}^\intercal \mathbf{\Phi}\mathbf{w}) = (\mathbf{\Phi}^\intercal \mathbf{\Phi})^{-1} \mathbf{\Phi}^\intercal \mathbf{\Phi} \text{E}(\mathbf{w}) = \mathbf{w} \end{align*}
Because
\begin{align*} \mathbf{\hat{w}} - \text{E}(\mathbf{\hat{w}}) & = (\mathbf{\Phi}^\intercal \mathbf{\Phi})^{-1} \mathbf{\Phi}^\intercal \mathbf{y} - (\mathbf{\Phi}^\intercal \mathbf{\Phi})^{-1} \mathbf{\Phi}^\intercal \mathbf{\Phi} \mathbf{w} = (\mathbf{\Phi}^\intercal \mathbf{\Phi})^{-1} \mathbf{\Phi}^\intercal (\mathbf{y} - \mathbf{\Phi} \mathbf{w}) \\ &\equiv (\mathbf{\Phi}^\intercal \mathbf{\Phi})^{-1} \mathbf{\Phi}^\intercal \epsilon \\ \text{E}(\epsilon \epsilon^\intercal) &= \text{Var}(\epsilon) = \sigma^2 \mathbf{I}_{n}, \end{align*}
the variance is
\begin{align*} \text{Var}(\mathbf{\hat{w}}) &= \text{E}((\mathbf{\hat{w}} - \text{E}(\mathbf{\hat{w}}))(\mathbf{\hat{w}} - \text{E}(\mathbf{\hat{w}}))^\intercal) = (\mathbf{\Phi}^\intercal \mathbf{\Phi})^{-1} \mathbf{\Phi}^\intercal \text{E}(\epsilon \epsilon^\intercal) \mathbf{\Phi} (\mathbf{\Phi}^\intercal \mathbf{\Phi})^{-1} \\ &= (\mathbf{\Phi}^\intercal \mathbf{\Phi})^{-1} \mathbf{\Phi}^\intercal \mathbf{\Phi} (\mathbf{\Phi}^\intercal \mathbf{\Phi})^{-1} \sigma^2 = (\mathbf{\Phi}^\intercal \mathbf{\Phi})^{-1} \sigma^2 \end{align*}
Theorem: \(\hat{\sigma}^2\) is an unbiased estimate of the variance \(\sigma^2\) where
\begin{align*} \hat{\sigma}^2 = \frac{1}{n-p} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 \text{ with } \hat{y}_i = f(\mathbf{x}_i,\mathbf{w}) \end{align*}
Proof:
The vector of residual
\begin{align*} \hat{\epsilon} = \mathbf{y} - \mathbf{\hat{y}} = \mathbf{y} - \mathbf{\Phi} \mathbf{w} = (\mathbf{I} - \mathbf{\Phi} (\mathbf{\Phi}^\intercal \mathbf{\Phi})^{-1} \mathbf{\Phi}^\intercal) \mathbf{y} \equiv Q \mathbf{y} = Q (\mathbf{X} \mathbf{w} + \epsilon) = Q \epsilon \end{align*}
Note that \(\textrm{tr}(Q) = n - p\) and \(Q^\intercal=Q=Q^2\). The eigenvalues of \(Q\) are therefore 0 and 1.
Since \(Q^2 - Q=0\), the minimal polynomial of \(Q\) divides the polynomial \(z^2 - z\). So, the eigenvalues of \(Q\) are among 0 and 1. Since \(\textrm{tr}(Q) = n - p\) is also the sum of the eigenvalues multiplied by their multiplicity, we necessarily have that 1 is an eigenvalue with multiplicity \(n - p\) and zero is an eigenvalue with multiplicity \(p\).
Since \(Q\) is real and symmetric, there exists an orthogonal matrix \(V\) with
\begin{align*} V^\intercal QV = \Delta = \textrm{diag}(\underbrace{1, \ldots, 1}_{n-p \textrm{ times}}, \underbrace{0, \ldots, 0}_{p \textrm{ times}}) \end{align*} We have \(\textrm{E}(\hat{\sigma}^2) = \textrm{E}(\hat{\epsilon}^\intercal \hat{\epsilon}) = \textrm{E}(\epsilon^\intercal Q \epsilon)\). Since \(\epsilon^\intercal Q \epsilon\) is \(1 \times 1\) matrix, so it is equal its trace.
\begin{align*} \textrm{E}(\epsilon^\intercal Q \epsilon) &= \textrm{E}(\textrm{tr}(\epsilon^\intercal Q \epsilon)) = \textrm{E}(\textrm{tr}(Q \epsilon \epsilon^\intercal)) = \textrm{tr}(Q\textrm{E}(\epsilon \epsilon^\intercal))\\ & = \textrm{tr}(Q\textrm{E}(\sigma^2 \mathbf{I})) = \sigma^2 \textrm{tr}(Q) = \sigma^2 (n-p) \end{align*}
If \(\hat{\epsilon} \sim N(0, \sigma^2 \mathbf{I})\), we let \(K \equiv V^\intercal \hat{\epsilon}\). Then \(K \sim N(0, \sigma^2 \Delta)\) with \(K_{n-p+1}=\ldots=K_n=0\) and
\begin{align*} \frac{\|K\|^2}{\sigma^2} &= \frac{\|K^{\star}\|^2}{\sigma^2} \sim \chi^2_{n-p} \end{align*}
with \(K^{\star} = (K_1, \ldots, K_{n-p})^\intercal\). Since \(V\) is orthogonal,
\begin{align*} \|\hat{\epsilon}\|^2 &= \|K\|^2=\|K^{\star}\|^2 \end{align*}
Thus,
\begin{align*} \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{\sigma^2} &\sim \chi^2_{n-p} \end{align*}
\(\blacksquare\)
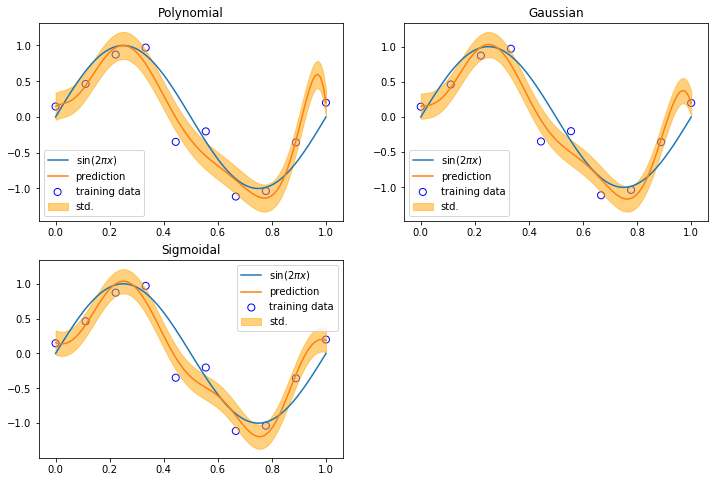
We use least squares to fit 10 input data points with different basis functions.
[3]:
x_train, t_train = create_data(sinusoidal, 10, 0.25)
x_test = np.linspace(0, 1, 100)
t_test = sinusoidal(x_test)
basis_funcs = {'Polynomial': [8], 'Gaussian': [np.linspace(0, 1, 8), 0.1], 'Sigmoidal': [np.linspace(0, 1, 8), 10]}
fig = plt.figure(figsize=(12, 8))
for i, (key, value) in enumerate(basis_funcs.items()):
phi_train = globals()[key](*value).dm(x_train)
phi_test = globals()[key](*value).dm(x_test)
t, t_std = LeastSquares().fit(phi_train, t_train).predict_dist(phi_test)
plt.subplot(2, 2, i+1)
plt.scatter(x_train, t_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, t_test, label="$\sin(2\pi x)$")
plt.plot(x_test, t, label="prediction")
plt.fill_between(x_test, t - t_std, t + t_std, color="orange", alpha=0.5, label="std.")
plt.title("{}".format(key))
plt.legend()
plt.show()
toggle()
[3]:
The case with multiple outputs (so far, we only consider \(y\) is a single-dimensional variable for each observation) is a natural generalization.
Geometrical Interpretation¶
The least-squares solution is obtained by finding the orthogonal projection of the data vector \(\mathbf{y}\) onto the subspace spanned by the basis \(\phi_j(\mathbf{x})\).
The regression can be performed by successive orthogonalization. The algorithm is known as Gram-Schmidt orthogonalization procedure, which is equivalent to the QR decomposition of \(\mathbf{X}\). If inputs are orthogonal, the regression process is independent for each feature.
Stochastic Gradient Descent¶
When the training data set is very large or received in a stream, a direct solution using the normal equations of the least squares may not be possible.
An alternative approach is the \textit{stochastic gradient descent} algorithm.
The total error function
\begin{align} E_{\mathcal{D}}(\mathbf{w}) & = \frac{1}{2} \sum_{i=1}^{n} (y_i - \mathbf{w}^\intercal \phi(x_{i}))^2 \equiv \sum_{i=1}^{n} E_{i}(\mathbf{w}) \nonumber \end{align}
In general, the stochastic gradient descent algorithm is applying
\begin{align} \mathbf{w}^{\tau + 1} = \mathbf{w}^\tau - \eta \bigtriangledown_{\mathbf{w}} E_i \nonumber \end{align} where \({\tau}\) is the iteration number and \(\eta\) is a learning rate parameter.
When the error function is the sum-of-squares function (the order of evaluation does not change the result), then the algorithm is
\begin{align} \mathbf{w}^{\tau + 1} = \mathbf{w}^\tau + \eta \left(y_i - \mathbf{w}^{(\tau) \intercal}\phi_i\right)\phi_i \nonumber \end{align}
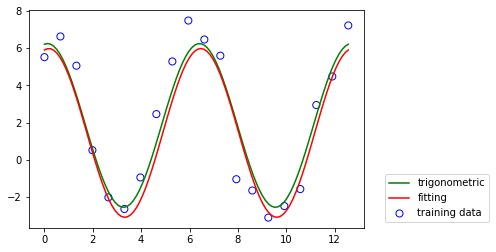
Data is generated by a trigonomietric function
\begin{align} t = w_0 + w_1 \sin(x) + w_2 \cos(x) \nonumber \end{align}
[4]:
def trigonometric(x, w=[1.85, 0.57, 4.37]):
return np.dot(w, [np.ones_like(x), np.sin(x), np.cos(x)])
x_trig_train, t_trig_train = create_data(trigonometric, 20, 1, [0, 4.0*np.pi])
x_trig_test = np.linspace(0, 4.0*np.pi, 100)
t_trig_test = trigonometric(x_trig_test)
# design matrix
phi = np.array([np.ones_like(x_trig_train), np.sin(x_trig_train), np.cos(x_trig_train)]).transpose()
# we set initial w = 0
w = np.zeros(phi.shape[1])
eta = 0.25
# since we have 20 samples, we use gradient from each sample in order
for i in range(20):
w = w + eta * (t_trig_train[i] - np.dot(w.T, phi[i])) * phi[i]
t_predicted = trigonometric(x_trig_test, w)
plt.scatter(x_trig_train, t_trig_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_trig_test, t_trig_test, c="g", label="trigonometric")
plt.plot(x_trig_test,t_predicted, c='r', label="fitting")
plt.legend(bbox_to_anchor=(1.05, 0.27), loc=2, borderaxespad=0.5)
plt.show()
toggle()
[4]:
Bias-Variance Decomposition¶
We seek a function \(f(\mathbf{x})\) for predicting \(y\) given the input \(\mathbf{x}\). Let \(h(\mathbf{x})\) be the conditional expectation, also known as the regression function where
\begin{align} h(\mathbf{x}) = \mathbb{E} (y \lvert \mathbf{x} ) = \int y p(y \lvert \mathbf{x}) dt \nonumber \end{align}
[5]:
hide_comment()
[5]:
The decision theory minimizes a loss function for penalizing errors in prediction
\begin{align*} \mathbb{E} (f) & = \int \int \left( f(\mathbf{x}) - y \right)^2 p(\mathbf{x}, y) d\mathbf{x} dy \end{align*}
By conditioning on \(\mathbf{x}\), we have
\begin{align*} \mathbb{E} (f) & = \mathbb{E} _{\mathbf{x}} \mathbb{E} _{y|\mathbf{x}} \left[ \left( f(\mathbf{x}) - y \right)^2 | \mathbf{x} \right] \end{align*}
It suffices to minimize the expected loss pointwise
\begin{align*} h(\mathbf{x}_0) = \text{argmin}_{\alpha} \mathbb{E} _{y|\mathbf{x}} \left[ \left(y - \alpha \right)^2 | \mathbf{x} = \mathbf{x}_0 \right] = \mathbb{E} (y \lvert \mathbf{x} = \mathbf{x}_0 ) \end{align*}
\(\blacksquare\)
From a frequentist perspective, if consider a single input value \(\mathbf{x}\), the expected loss is
\begin{align*} \mathbb{E} (L_{\mathbf{x}}) & = \int \int \left( f(\mathbf{x}) - y \right)^2 p(\mathbf{x}, y) d\mathbf{x} dy \end{align*}
The above squared loss function arising from decision theory. However, the sum-of-squares error function that arose in the maximum likelihood estimation of model parameters.
For a particular data set \(\mathcal D\), \(f(\mathbf{x})\) takes the form \(f(\mathbf{x}; \mathcal D)\).
\begin{align*} \mathbb{E} (L_{\mathbf{x}}) = \underbrace{\mathbb{E}_{\mathcal D}\left[ \left( f(\mathbf{x}; \mathcal D) - \mathbb{E}_{\mathcal D}\left[ f(\mathbf{x}; \mathcal D)\right] \right)^2 \right]}_{\text{variance}} + \underbrace{\left( \mathbb{E}_{\mathcal D}\left[f(\mathbf{x}; \mathcal D)\right] - h(\mathbf{x}) \right)^2}_{\text{bias$^2$}} + \underbrace{\int \text{Var}\left[y|\mathbf{x}\right] p(\mathbf{x}) d\mathbf{x}}_{\text{noise}} \end{align*}
or
\begin{equation*} \text{expected loss = variance (of prediction) + bias$^2$ (of estimate) + noise (of data)} \label{bias_var_decomp} \end{equation*}
[6]:
hide_comment()
[6]:
\begin{align*} \mathbb{E} (L_{\mathbf{x}}) & = \int \int \left( f(\mathbf{x}) - y\right)^2 p(\mathbf{x}, y) d\mathbf{x} dy \\ & = \int \int \left( f(\mathbf{x}) - \mathbb{E} \left[ y | \mathbf{x}\right] + \mathbb{E} \left[ y | \mathbf{x}\right] - y \right)^2 p(\mathbf{x}, t) d\mathbf{x} dy \\ & = \int \int \left( ( f(\mathbf{x}) - \mathbb{E} \left[ y | \mathbf{x}\right] )^2 + \underbrace{2 ( f(\mathbf{x}) - \mathbb{E} \left[ y | \mathbf{x}\right] )(\mathbb{E} \left[ y | \mathbf{x}\right] -y)}_{\text{vanishes}} + (\mathbb{E} \left[ y | \mathbf{x}\right] - y )^2\right) p(\mathbf{x}, y) d\mathbf{x} dy \\ & = \int \left( f(\mathbf{x}) - \mathbb{E} \left[ y | \mathbf{x}\right] \right)^2 p(\mathbf{x}) d\mathbf{x} + \int \left( \mathbb{E} \left[ y | \mathbf{x}\right] -y \right)^2 p(\mathbf{x},y) d\mathbf{x} dy \\ & = \int \left( f(\mathbf{x}) - h(\mathbf{x}) \right)^2 p(\mathbf{x}) d\mathbf{x} + \underbrace{\int \text{Var}\left[y|\mathbf{x}\right] p(\mathbf{x}) d\mathbf{x}}_{\text{noise}} \end{align*}
For any given data set \(\mathcal{D}\), learning algorithm obtains a prediction function \(y(\mathbf{x}; \mathcal{D})\).
The term is vanished because
\begin{align*} \int ( y(\mathbf{x}) - \mathbb{E} \left[ y | \mathbf{x}\right] ) \mathbb{E} \left[ y | \mathbf{x}\right] p(\mathbf{x},y) d\mathbf{x} dy &= \int ( y(\mathbf{x}) - \mathbb{E} \left[ y | \mathbf{x}\right] ) \mathbb{E} \left[ y | \mathbf{x}\right] p(\mathbf{x}) p(y|\mathbf{x})d\mathbf{x} dy \\ & = \int ( y(\mathbf{x}) - \mathbb{E} \left[ y | \mathbf{x}\right] ) \mathbb{E} \left[ y | \mathbf{x}\right] p(\mathbf{x}) (\int p(y|\mathbf{x}) dy)d\mathbf{x} \\ & =\int ( y(\mathbf{x}) - \mathbb{E} \left[ y | \mathbf{x}\right] ) \mathbb{E} \left[ y | \mathbf{x}\right] p(\mathbf{x}) d\mathbf{x} \\ \int ( y(\mathbf{x}) - \mathbb{E} \left[ y | \mathbf{x}\right] ) y p(\mathbf{x},y) d\mathbf{x} dy &= \int ( y(\mathbf{x}) - \mathbb{E} \left[ y | \mathbf{x}\right] ) y p(\mathbf{x}) p(y|\mathbf{x}) d\mathbf{x} dy \\ & = \int ( y(\mathbf{x}) - \mathbb{E} \left[ y | \mathbf{x}\right] ) p(\mathbf{x}) (\int y p(y|\mathbf{x}) dy ) d\mathbf{x} \\ & = \int ( y(\mathbf{x}) - \mathbb{E} \left[ y | \mathbf{x}\right] ) \mathbb{E} \left[ y | \mathbf{x}\right] p(\mathbf{x}) d\mathbf{x} \end{align*}
Now, we consider
\begin{align*} \int \left( f(\mathbf{x}) - h(\mathbf{x}) \right)^2 p(\mathbf{x}) d\mathbf{x} \end{align*}
We have \begin{align*} \left( f(\mathbf{x}; \mathcal D) - h(\mathbf{x}) \right)^2 =& \left( f(\mathbf{x}; \mathcal D) - \mathbb{E}_{\mathcal D}\left[ f(\mathbf{x}; \mathcal D)\right] + \mathbb{E}_{\mathcal D}\left[f(\mathbf{x}; \mathcal D)\right] - h(\mathbf{x}) \right)^2 \\ &= \left( f(\mathbf{x}; \mathcal D) - \mathbb{E}_{\mathcal D}\left[ f(\mathbf{x}; \mathcal D)\right] \right)^2 + \left( \mathbb{E}_{\mathcal D}\left[f(\mathbf{x}; \mathcal D)\right] - h(\mathbf{x}) \right)^2 \\ &\hspace{1cm} + \underbrace{2 \left( f(\mathbf{x}; \mathcal D) - \mathbb{E}_{\mathcal D}\left[ f(\mathbf{x}; \mathcal D)\right] \right) \left( \mathbb{E}_{\mathcal D}\left[f(\mathbf{x}; \mathcal D)\right] - h(\mathbf{x}) \right)}_{\text{vanishes after taking $\mathbb{E}_{\mathcal D}$}} \end{align*}
We get mean squared error (MSE)
\begin{align*} \mathbb{E}_{\mathcal D}\left[ \left( f(\mathbf{x}; \mathcal D) - h(\mathbf{x}) \right)^2 \right] = \underbrace{\mathbb{E}_{\mathcal D}\left[ \left( f(\mathbf{x}; \mathcal D) - \mathbb{E}_{\mathcal D}\left[ f(\mathbf{x}; \mathcal D)\right] \right)^2 \right]}_{\text{variance}} + \underbrace{\left( \mathbb{E}_{\mathcal D}\left[f(\mathbf{x}; \mathcal D)\right] - h(\mathbf{x}) \right)^2}_{\text{bias$^2$}} \end{align*}
\(\blacksquare\)
Bias-Variance Decomposition provide insights on model complexity from a frequentist perspective.
Noise cannot be reduced because it exists in the true data generation process.
Bias-variance trade-off shows that very flexible models has low bias and high variance, but relatively rigid models has high bias and low variance.
For example, least squares estimates \(\mathbf{w}\) has the smallest variance among all linear unbiased estimates (Gauss-Markov Theorem). However, biased estimates (e.g., ridge regression) may have smaller variance.
The bias-variance trade-off is demonstrated by \(k\)-nearest-neighbor regression and linear regression
[7]:
hide_comment()
[7]:
Consider \(y = f(\mathbf{x}) + \epsilon\) where \(\mathbb{E}(\epsilon) = 0\) and \(\text{Var}(\epsilon) = \sigma^2\).
For :math:`k`-nearest-neighbor regression fit
\begin{align*} \hat{f}(\mathbf{x}) = \text{Avg} (y_i | \mathbf{x}_i \in N_{k} (\mathbf{x})), \end{align*}
where \(N_{k} (\mathbf{x})\) is the neighborhood containing the \(k\) points in the training dataset closest to \(\mathbf{x}\), the expected loss has the form
\begin{align*} \mathbb{E}(L_{\mathbf{x}_0}) &= \mathbb{E} \left[ (y - \hat{f}(\mathbf{x}_0))^2| \mathbf{x} = \mathbf{x}_0 \right]\\ & = \sigma^2 + \left[ f(\mathbf{x}_0) - \frac{1}{k} \sum_{\ell = 1}^{k} f(\mathbf{x}_{(\ell)})\right]^2 + \frac{\sigma^2}{k} \end{align*}
For a linear regression model
\begin{align*} \hat{f}_p(\mathbf{x}) = \mathbf{x}^\intercal \beta, \end{align*}
where \(\beta\) has \(p\) components, we have
\begin{align*} \mathbb{E}(L_{\mathbf{x}_0}) &= \mathbb{E} \left[ (y - \hat{f}(\mathbf{x}_0))^2| \mathbf{x} = \mathbf{x}_0 \right]\\ & = \sigma^2 + \left[ f(\mathbf{x}_0) - \mathbb{E} \hat{f}_p(\mathbf{x}_0) \right]^2 + \|\mathbf{X}(\mathbf{X}^\intercal \mathbf{X})^{-1} \mathbf{x}_0 \|^2\sigma^2 \end{align*}
Note the fit
\begin{align*} \hat{f}_p(\mathbf{x}_0) = \mathbf{x}^\intercal \beta = \mathbf{x}^\intercal (\mathbf{X}^\intercal \mathbf{X})^{-1} \mathbf{X}^\intercal y, \end{align*}
and hence
\begin{align*} \text{Var}(\hat{f}_p(\mathbf{x}_0)) = \|\mathbf{X}(\mathbf{X}^\intercal \mathbf{X})^{-1} \mathbf{x}_0 \|^2\sigma^2 \end{align*}
\(\blacksquare\)
The bias-variance trade-off plays an important role in frequentist view. However, the insights on model complexity is of limited practical value, because
the bias-variance decomposition is based on averages, \(\mathbb{E}_{\mathcal D}\), with respect to several data sets, whereas in practice we have only the single observed data set.
if we had a large number of independent training sets, we would be better off combining them, which of course would reduce the level of over-fitting for a given model complexity.
There are two reasons why we are not satisfied with the least squares estimates:
Interpretation: instead of having a large number of predictors, we like to determine a smaller subset that exhibit the strongest effects.
Prediction accuracy: the least squares estimates often have low bias but large variance. Prediction accuracy can sometimes be improved by shrinking or setting some coefficients to zero.
Next, we will regularize regression models with some constraints. The constraints may add bias to the model, but the resulting model will have lower variance.
Subset Selection¶
We only consider a subset of the independent variables, and eliminate the rest from the model. Least squares regression is used to estimate the coefficients of the inputs that are retained.
Best subset regression finds for each subset size \(k\) that gives smallest residual sum of squares \(\text{RSS}(\mathbf{w})\).
Forward- and Backward-Stepwise Selection are greedy algorithms to find a subset of variables by producing a nested sequence of models.
Forward stepwise selection starts with the intercept, and then sequentially adds into the model the predictor that most improves the fit in terms of \(\text{RSS}(\mathbf{w})\).
Backward-stepwise selection starts with the full model, and sequentially deletes the predictor that has the least impact on the fit. The candidate for dropping is the variable with the smallest Z-score.
Forward-Stagwise Selection is even more constrained than forward stepwise regression as follows
Choose \(\mathbf{x}_j\) with highest current correlation \(c_j = \mathbf{x}_j^\intercal(\mathbf{y} - \mathbf{\hat{y}})\)
Take a small step \(0 < \alpha < |c_j|\) in the direction of selected \(\mathbf{x}_j\)
\(\hat{y} \leftarrow \hat{y} + \alpha \cdot \text{sign}(c_j) \cdot \mathbf{x}_j\)
By retaining a subset of the predictors and discarding the rest, subset selection produces a model that is interpretable and has possibly lower prediction error than the full model. However, because it is a discrete process that variables are either retained or discarded. It often exhibits high variance, and sometimes doesn’t reduce the prediction error of the full model.
Shrinkage Methods¶
Shrinkage methods are more continuous by shrinking the regression coefficients by imposing a penalty on their size, and don’t suffer as much from high variability.
\begin{align*} E_{\mathcal{D}}(\mathbf{w}) + \lambda E_{\mathbf{w}}(\mathbf{w}) & = \frac{1}{2} \sum_{i=1}^{n} (y_i - \mathbf{w}^\intercal \phi(x_{i}))^2 + \frac{\lambda}{2} \sum_{i=0}^{m} \lvert w_i \rvert^q \\ & = \frac{1}{2} \left( \mathbf{y}^\intercal \mathbf{y} - 2 (\mathbf{\Phi} \mathbf{w})^\intercal \mathbf{y} + (\mathbf{\Phi} \mathbf{w})^\intercal \mathbf{\Phi} \mathbf{w} \right) + \frac{\lambda}{2} \lVert \mathbf{w} \rVert_q \end{align*}
It is equivalent to minimize the unregularized sum-of-squares error subject to the constraint
\begin{align*} \sum_{i=0}^{n} \lvert w_i \rvert^q \le \eta. \end{align*}
Examples:
\(q=0\) is variable subset selection,
\(q=1\) is know as the lasso (Least Absolute Shrinkage and Selection Operator), and
\(q=2\) corresponds to ridge regression. We have
\begin{align*} E_{\mathcal{D}}(\mathbf{w}) + \lambda E_{\mathbf{w}}(\mathbf{w}) & \sim (\mathbf{\Phi} \mathbf{w})^\intercal \mathbf{\Phi} \mathbf{w} - 2 (\mathbf{\Phi} \mathbf{w})^\intercal \mathbf{y} + \mathbf{y}^\intercal \mathbf{y} + \lambda (\mathbf{I} \mathbf{w})^\intercal \mathbf{w} \\ \frac{d (E_{\mathcal{D}}(\mathbf{w}) + E_{\mathbf{w}}(\mathbf{w}) )}{d \mathbf{w}} & = 2\mathbf{\Phi}^\intercal \mathbf{\Phi} \mathbf{w} - 2\mathbf{\Phi}^\intercal \mathbf{y} + 2\lambda \mathbf{I} \mathbf{w} = 0 \\ \mathbf{\Phi}^\intercal \mathbf{y} &= \left( \mathbf{\Phi}^\intercal \mathbf{\Phi} + \lambda \mathbf{I} \right) \mathbf{w} \\ \mathbf{w} &= \left(\mathbf{\Phi}^\intercal \mathbf{\Phi} + \lambda \mathbf{I} \right)^{-1} \mathbf{\Phi}^\intercal \mathbf{y} \end{align*}
One might consider estimating \(q\) from data, however it is not worth the effort for the extra variance incurred.
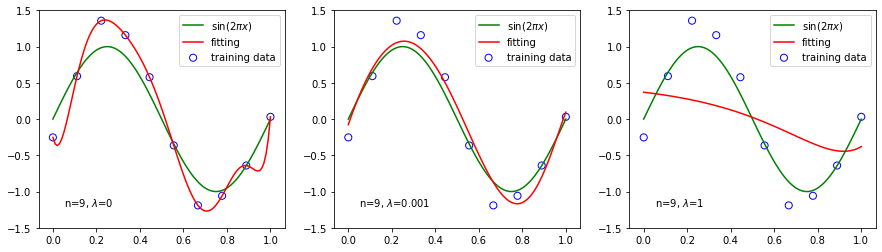
We use ridge regression with three different values for a polynomial fitting.
[8]:
x_train, t_train = create_data(sinusoidal, 10, 0.25)
x_test = np.linspace(0, 1, 100)
t_test = sinusoidal(x_test)
# set degree = 9 because it's the most complicated polynomial model for 10 data points
phi_train = Polynomial(9).dm(x_train)
phi_test = Polynomial(9).dm(x_test)
fig = plt.figure(figsize=(15, 4))
for i, alpha in enumerate([0, 1e-3, 1]):
# alpha is the regularization coefficient
t = LeastSquares(alpha).fit(phi_train, t_train).predict(phi_test)
plt.subplot(1, 3, i+1)
plt.scatter(x_train, t_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, t_test, c="g", label="$\sin(2\pi x)$")
plt.plot(x_test, t, c="r", label="fitting")
plt.ylim(-1.5, 1.5)
plt.legend(loc=1)
plt.annotate(r"n={}, $\lambda$={}".format(9, alpha), xy=(0.05, -1.2))
plt.show()
toggle()
[8]:
Bias-Variance Trade off¶
We illustrate bias and variance with a regularization parameter \(\ln \lambda \in \{2.6, -0.31, -2.4\}\).
In
x_train, t_train, we generate 100 datasets, and each has 25 sinusoidal data pointsGraphs in the first row demonstrate variance
\begin{align*} \mathbb{E}_{\mathcal D}\left[ \left( f(\mathbf{x}; \mathcal D) - \mathbb{E}_{\mathcal D}\left[ f(\mathbf{x}; \mathcal D)\right] \right)^2 \right] \end{align*}
where each curve is represented by a function \(f(\mathbf{x}; \mathcal D)\) with given dataset \(\mathcal D\). When \(\mathcal D\) is given, \(f(\mathbf{x}; \mathcal D)\) is a fitting function based on the dataset (for clarity, only 20 of the 100 fits are shown). Their average \(\mathbb{E}_{\mathcal D}\left[ f(\mathbf{x}; \mathcal D)\right]\) gives the fitting curve of graphs in the second row.
Thus, graphs in the second row demonstrate bias\(^2\)
\begin{align*} \left( \mathbb{E}_{\mathcal D}\left[f(\mathbf{x}; \mathcal D)\right] - h(\mathbf{x}) \right)^2 \end{align*}
where \(h(\mathbf{x})\) the optimal prediction, i.e., \(\sin (2 \pi x)\) in our case.
The last graph shows variance and bias\(^2\) by varying \(\lambda\).
[9]:
funcs = {'Polynomial': [24], 'Gaussian': [np.linspace(0, 1, 24), 0.1], 'Sigmoidal': [np.linspace(0, 1, 24), 10]}
x_test = np.linspace(0, 1, 100)
t_test = sinusoidal(x_test)
def bias_and_var(fname):
phi_test = globals()[fname](*funcs[fname]).dm(x_test)
plt.figure(figsize=(12, 6))
for loc, alpha in enumerate([2.6, -0.31, -2.4]):
plt.subplot(2, 3, loc+1)
# We have 100 data sets, each having 25 data points
x_train, t_train = zip(*[create_data(sinusoidal, 25, 0.8) for i in range(100)])
phi_train = [globals()[fname](*funcs[fname]).dm(x) for x in x_train]
# t[i] is an array contains the prediction values for x_test and
# the fitting function is derived based on i-th data set
t = [LeastSquares(np.exp(alpha)).fit(phi, t).predict(phi_test) for phi, t in zip(phi_train, t_train)]
# For clarity, only 20 of the 100 fits are shown
for i in range(20):
plt.plot(x_test, t[i], c="orange")
plt.annotate(r"$\ln \lambda={}$".format(alpha), xy=(0.05, -1.2))
plt.ylim(-1.5, 1.5)
plt.subplot(2, 3, loc+4)
plt.plot(x_test, t_test, c="g", label="$\sin(2\pi x)$")
plt.plot(x_test, np.asarray(t).mean(axis=0), c="r", label="fitting")
plt.ylim(-1.5, 1.5)
plt.legend()
plt.show()
plt.figure(figsize=(6, 5))
x_train, t_train = zip(*[create_data(sinusoidal, 25, 0.8) for i in range(100)])
phi_train = [globals()[fname](*funcs[fname]).dm(x) for x in x_train]
alpha_range = np.linspace(-2.6, 1.5, 30)
t = [[LeastSquares(np.exp(alpha)).fit(phi, t).predict(phi_test) for phi, t in zip(phi_train, t_train)]
for alpha in alpha_range]
bias2 = ((np.asarray(t).mean(axis=1) - t_test) ** 2).mean(axis=1) #(3.46)
var = np.array(t).var(axis=1).mean(axis=1) #(3.47)
plt.ylim(0, (bias2+var).max()+.01)
plt.plot(alpha_range, bias2, label=r"bias$^2$")
plt.plot(alpha_range, var, label="var")
plt.plot(alpha_range, bias2+var, label=r"bias$2$+var")
plt.xlabel('$\ln \lambda$')
plt.legend()
plt.show()
toggle()
[9]:
[10]:
widget_layout = widgets.Layout(width='250px', height='30px')
interact(bias_and_var,
fname = widgets.Dropdown(description='Basis Functions:',
style = {'description_width': 'initial'},
options=['Polynomial','Gaussian','Sigmoidal'],
value='Gaussian',layout=widget_layout));
Singular Value Decomposition¶
The singular value decomposition (SVD) of \(\mathbf{X}_{n \times p} = (\mathbf{x}_1, \ldots, \mathbf{x}_n)^\intercal\) has the form \(\mathbf{X} = U D V^\intercal\), where
\(U_{n \times p}\) is orthogonal and the columns are spanning the column space of \(\mathbf{X}\)
\(V_{p \times p}\) is orthogonal and the columns are spanning the row space of \(\mathbf{X}\)
\(D_{p \times p}\) is diagonal with \(d_1 \ge d_2 \ge \cdots \ge d_p \ge 0\).
We have
\begin{align*} \mathbf{X} \mathbf{w}^{\text{ls}} = UU^\intercal \mathbf{y} = \sum_{j=1}^{p} \mathbf{u}_j (\mathbf{u}^\intercal_j \mathbf{y}) \end{align*}
and
\begin{align*} \mathbf{X} \mathbf{w}^{\text{ridge}} = \sum_{j=1}^{p} \mathbf{u}_j \left(\frac{d^2_j}{d^2_j + \lambda} (\mathbf{u}^\intercal_j \mathbf{y}) \right) \end{align*}
where
\(\mathbf{u}_j\) is a normalized principle component,
Ridge shrinks more with smaller \(d^2_j\) (small variance),
Ridge improves interpretability by putting low weights on small variance components.
[11]:
hide_comment()
[11]:
Note that \(\mathbf{X}^\intercal \mathbf{X} = VDU^\intercal UDV^\intercal = VD^2V^\intercal\). Thus
\begin{align*} \mathbf{X} \mathbf{w}^{\text{ls}} &= UDV^\intercal (VD^2V^\intercal)^{-1} VDU^\intercal \mathbf{y} = UDV^\intercal (V^{-\intercal}D^{-2}V^{-1}) VDU^\intercal \mathbf{y} \\ &= UU^\intercal \mathbf{y} = \sum_{j=1}^{p} \mathbf{u}_j (\mathbf{u}^\intercal_j \mathbf{y}) \\ \mathbf{w}^{\text{ridge}} &= (\mathbf{X}^\intercal \mathbf{X} + \lambda \mathbf{I})^{-1} \mathbf{X}^\intercal \mathbf{y} = (VD^2V^\intercal + \lambda VV^\intercal)^{-1}VDU^\intercal\mathbf{y} \\ &= (V(D^2+\lambda \mathbf{I})V^\intercal)^{-1}VDU^\intercal\mathbf{y} \\ &= V^{-\intercal}(D^2+\lambda \mathbf{I})^{-1}DU^\intercal\mathbf{y} \\ \mathbf{X} \mathbf{w}^{\text{ridge}} &=UD(D^2+\lambda \mathbf{I})^{-1}DU^\intercal\mathbf{y} \end{align*}
The matrix \(D(D^2+\lambda \mathbf{I})^{-1}D\) is diagonal with elements given by
\begin{align*} \frac{d^2_j}{d^2_j + \lambda} \end{align*}
Thus,
\begin{align*} \mathbf{X} \mathbf{w}^{\text{ridge}} &= \sum_{j=1}^{p} \mathbf{u}_j \left(\frac{d^2_j}{d^2_j + \lambda} (\mathbf{u}^\intercal_j \mathbf{y}) \right) \end{align*}
\(\blacksquare\)
Principal Components Regression¶
In many situations we have a large number of inputs, often very correlated. We create a small number of new variables which are linear combinations of the original inputs. Then those new variables are used in place of the original inputs in the regression.
Principal Components Regression (PCR) forms the derived input columns (principle components) and then regresses \(y\) on a subset of those components.
The main purposes of a principal component analysis are the analysis of data to identify patterns and finding patterns to reduce the dimensions of the dataset with minimal loss of information.
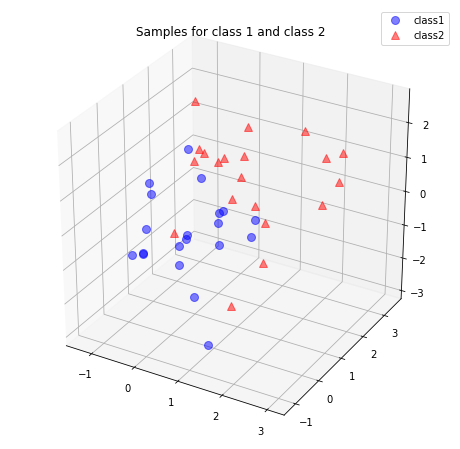
We start with a 3-dimensional dataset that we reduce to an 2-dimensional dataset by dropping 1 dimension.
We generate 40 3-dimensional samples randomly drawn from a multivariate Gaussian distribution. Assume that the samples stem from two different classes, where one half (i.e., 20) samples of our data set are labeled \(\mathcal{C}_1\) (class 1) and the other half \(\mathcal{C}_2\) (class 2) with mean vectors
\begin{align*} \mu_1 = \mu_2 = \begin{bmatrix}0\\0\\0\end{bmatrix} \end{align*}
and covariance matrices \begin{align*} \Sigma_1 = \Sigma_2 = \begin{bmatrix}1\quad 0\quad 0\\0\quad 1\quad0\\0\quad0\quad1\end{bmatrix} \end{align*}
[12]:
import numpy as np
np.random.seed(234)
mu_vec1 = np.array([0,0,0])
cov_mat1 = np.array([[1,0,0],[0,1,0],[0,0,1]])
class1_sample = np.random.multivariate_normal(mu_vec1, cov_mat1, 20).T
assert class1_sample.shape == (3,20), "The matrix has not the dimensions 3x20"
mu_vec2 = np.array([1,1,1])
cov_mat2 = np.array([[1,0,0],[0,1,0],[0,0,1]])
class2_sample = np.random.multivariate_normal(mu_vec2, cov_mat2, 20).T
assert class2_sample.shape == (3,20), "The matrix has not the dimensions 3x20"
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d import proj3d
fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(111, projection='3d')
plt.rcParams['legend.fontsize'] = 10
ax.plot(class1_sample[0,:], class1_sample[1,:], class1_sample[2,:], 'o',
markersize=8, color='blue', alpha=0.5, label='class1')
ax.plot(class2_sample[0,:], class2_sample[1,:], class2_sample[2,:], '^',
markersize=8, alpha=0.5, color='red', label='class2')
plt.title('Samples for class 1 and class 2')
ax.legend(loc='upper right')
plt.show()
toggle()
[12]:
We created two \(3 \times 20\) datasets - one dataset for each class - where each column can be pictured as a 3-dimensional vector
\begin{align*} \pmb x = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} \end{align*}
so that our dataset will have the form \begin{align*} \pmb X = \begin{pmatrix} x_{1_1}\; x_{1_2} \; ... \; x_{1_{20}}\\ x_{2_1} \; x_{2_2} \; ... \; x_{2_{20}}\\ x_{3_1} \; x_{3_2} \; ... \; x_{3_{20}}\end{pmatrix} \end{align*}
Because we don’t need class labels for the PCA, let us merge the samples for our 2 classes into one \(3 \times 40\)-dimensional array.
[13]:
all_samples = np.concatenate((class1_sample, class2_sample), axis=1)
Computing the Mean Vector Scatter Matrix¶
The \(p\)-dimensional mean vector is
[14]:
mean_x = np.mean(all_samples[0,:])
mean_y = np.mean(all_samples[1,:])
mean_z = np.mean(all_samples[2,:])
mean_vector = np.array([[mean_x],[mean_y],[mean_z]])
print('Mean Vector:\n', mean_vector)
Mean Vector:
[[0.77257186]
[0.68324797]
[0.43460518]]
The scatter matrix is computed by the following equation \begin{align*} S = \sum\limits_{k=1}^n (\pmb x_k - \pmb m)\;(\pmb x_k - \pmb m)^\intercal \end{align*}
where \(\pmb m\) is the mean vector \begin{align*} \pmb m = \frac{1}{n} \sum\limits_{k=1}^n \; \pmb x_k \end{align*}
or alternatively scatter_matrix = np.cov(all_samples) * (40 - 1) the covariance matrix \(\times\) \((n-1)\).
[15]:
scatter_matrix = np.zeros((3,3))
for i in range(all_samples.shape[1]):
scatter_matrix += (all_samples[:,i].reshape(3,1) - mean_vector).dot((all_samples[:,i].reshape(3,1) - mean_vector).T)
print('Scatter Matrix:\n', scatter_matrix)
Scatter Matrix:
[[39.35126181 4.22467775 12.74899364]
[ 4.22467775 50.9168567 10.18400644]
[12.74899364 10.18400644 66.86899978]]
Computing Eigenpairs¶
[16]:
eig_val_sc, eig_vec_sc = np.linalg.eig(scatter_matrix)
for i in range(len(eig_val_sc)):
eigvec_sc = eig_vec_sc[:,i].reshape(1,3).T
print('Eigenvector {}: \n{}'.format(i+1, eigvec_sc))
print('Eigenvalue {} from scatter matrix: {}'.format(i+1, eig_val_sc[i]))
print(40 * '-')
Eigenvector 1:
[[0.33730459]
[0.39443594]
[0.85477828]]
Eigenvalue 1 from scatter matrix: 76.59928002932904
----------------------------------------
Eigenvector 2:
[[ 0.93260098]
[-0.01618419]
[-0.36054609]]
Eigenvalue 2 from scatter matrix: 34.349151694294285
----------------------------------------
Eigenvector 3:
[[ 0.12837844]
[-0.91878091]
[ 0.37331034]]
Eigenvalue 3 from scatter matrix: 46.188686560075034
----------------------------------------
Visualizing the eigenvectors: we plot the eigenvectors centered at the sample mean.
[17]:
from matplotlib.patches import FancyArrowPatch
class Arrow3D(FancyArrowPatch):
def __init__(self, xs, ys, zs, *args, **kwargs):
FancyArrowPatch.__init__(self, (0,0), (0,0), *args, **kwargs)
self._verts3d = xs, ys, zs
def draw(self, renderer):
xs3d, ys3d, zs3d = self._verts3d
xs, ys, zs = proj3d.proj_transform(xs3d, ys3d, zs3d, renderer.M)
self.set_positions((xs[0],ys[0]),(xs[1],ys[1]))
FancyArrowPatch.draw(self, renderer)
fig = plt.figure(figsize=(7,7))
ax = fig.add_subplot(111, projection='3d')
ax.plot(all_samples[0,:], all_samples[1,:], all_samples[2,:], 'o', markersize=8, color='green', alpha=0.2)
ax.plot([mean_x], [mean_y], [mean_z], 'o', markersize=10, color='red', alpha=0.5)
for v in eig_vec_sc.T:
a = Arrow3D([mean_x, v[0]], [mean_y, v[1]], [mean_z, v[2]], mutation_scale=20, lw=3, arrowstyle="-|>", color="r")
ax.add_artist(a)
ax.set_xlabel('x_values')
ax.set_ylabel('y_values')
ax.set_zlabel('z_values')
plt.title('Eigenvectors')
plt.show()
toggle()
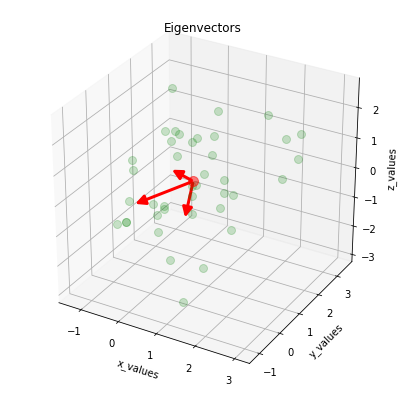
[17]:
Choosing \(k\) Largest Eigenvalues¶
We are reducing a 3-dimensional feature space to a 2-dimensional feature subspace by combining the two eigenvectors with the highest eigenvalues to construct our \(p \times k\)-dimensional eigenvector matrix \(\mathbf{W}\).
[18]:
eig_pairs = [(np.abs(eig_val_sc[i]), eig_vec_sc[:,i]) for i in range(len(eig_val_sc))]
# Sort the (eigenvalue, eigenvector) tuples from high to low
eig_pairs.sort(key=lambda x: x[0], reverse=True)
eig_pairs
[18]:
[(76.59928002932904, array([0.33730459, 0.39443594, 0.85477828])),
(46.188686560075034, array([ 0.12837844, -0.91878091, 0.37331034])),
(34.349151694294285, array([ 0.93260098, -0.01618419, -0.36054609]))]
[19]:
matrix_w = np.hstack((eig_pairs[0][1].reshape(3,1), eig_pairs[1][1].reshape(3,1)))
print('Matrix W:\n', matrix_w)
Matrix W:
[[ 0.33730459 0.12837844]
[ 0.39443594 -0.91878091]
[ 0.85477828 0.37331034]]
Transforming the Samples¶
In the last step, we use the \(2 \times 3\)-dimensional matrix \(\mathbf{W}\) that we just computed to transform our samples onto the new subspace via the equation
\begin{align*} y = \mathbf{W}^\intercal \mathbf{x} \end{align*}
[20]:
transformed = matrix_w.T.dot(all_samples)
plt.plot(transformed[0,0:20], transformed[1,0:20], 'o', markersize=7, color='blue', alpha=0.5, label='class1')
plt.plot(transformed[0,20:40], transformed[1,20:40], '^', markersize=7, color='red', alpha=0.5, label='class2')
plt.xlim([-4,4])
plt.ylim([-4,4])
plt.xlabel('x_values')
plt.ylabel('y_values')
plt.legend()
plt.title('Transformed samples with class labels')
plt.show()
toggle()
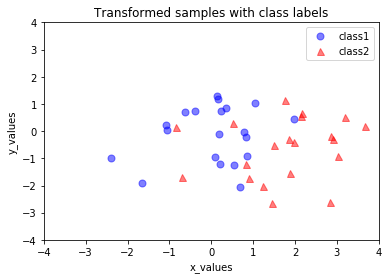
[20]:
Summary¶
Now, that we have seen how a principal component analysis works, we can use the PCA class from the scikit-learn machine-learning library for our convenience in future applications.
[21]:
from sklearn.decomposition import PCA as sklearnPCA
sklearn_pca = sklearnPCA(n_components=2)
sklearn_transf = sklearn_pca.fit_transform(all_samples.T)
plt.plot(sklearn_transf[0:20,0],sklearn_transf[0:20,1], 'o',
markersize=7, color='blue', alpha=0.5, label='class1')
plt.plot(sklearn_transf[20:40,0], sklearn_transf[20:40,1], '^',
markersize=7, color='red', alpha=0.5, label='class2')
plt.xlabel('x_values')
plt.ylabel('y_values')
plt.xlim([-4,4])
plt.ylim([-4,4])
plt.legend()
plt.title('Transformed samples with class labels from matplotlib.mlab.PCA()')
plt.show()
toggle()
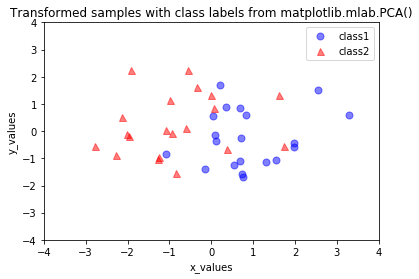
[21]:
If we want to mimic the results produced by scikit-learn, we need change the signs of the eigenvectors produced by scikit-learn
sklearn_transf = sklearn_transf * (-1)
and subtract the mean vectors from the samples \(\mathbf{X}\) to center the data at the coordinate system’s origin
transformed = matrix_w.T.dot(all_samples - mean_vector)
[22]:
sklearn_transf = sklearn_transf * (-1)
# sklearn.decomposition.PCA
plt.subplots(1, 2, figsize=(15,5))
plt.subplot(1, 2, 1)
plt.plot(sklearn_transf[0:20,0],sklearn_transf[0:20,1], 'o',
markersize=7, color='blue', alpha=0.5, label='class1')
plt.plot(sklearn_transf[20:40,0], sklearn_transf[20:40,1], '^',
markersize=7, color='red', alpha=0.5, label='class2')
plt.xlabel('x_values')
plt.ylabel('y_values')
plt.xlim([-4,4])
plt.ylim([-4,4])
plt.legend()
plt.title('Transformed samples via sklearn.decomposition.PCA')
# user-definied PCA
plt.subplot(1, 2, 2)
transformed = matrix_w.T.dot(all_samples - mean_vector)
plt.plot(transformed[0,0:20], transformed[1,0:20], 'o',
markersize=7, color='blue', alpha=0.5, label='class1')
plt.plot(transformed[0,20:40], transformed[1,20:40], '^',
markersize=7, color='red', alpha=0.5, label='class2')
plt.xlim([-4,4])
plt.ylim([-4,4])
plt.xlabel('x_values')
plt.ylabel('y_values')
plt.legend()
plt.title('Transformed samples step by step approach')
plt.show()
toggle()
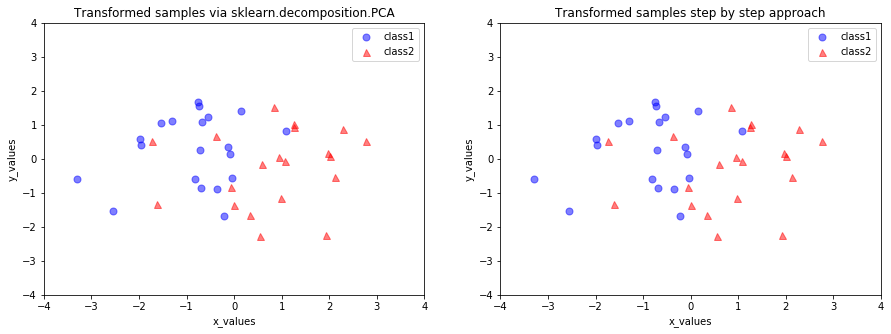
[22]:
In PCR, we are interested to find the directions (components) that maximize the variance in our dataset. The implicit assumption is that the response will tend to vary most in the directions of high variance of the inputs. Therefore, we project the entire set of data (without class labels) onto a different subspace via PCA and identify some important predictors.
Partial Least Squares¶
This technique also constructs a set of linear combinations of the inputs for regression, but unlike principal components regression it uses \(\mathbf y\) (in addition to \(\mathbf X\)) for this construction.
Both PLS and PCR are not scale invariant, so we need to standardize input \(\mathbf{x}_j\) to have mean \(0\) and variance \(1\).
Relation to the optimization problem
PLS seeks direction that have high variance and have high correlation with the response, in contrast to PCR with keys only on high variance (Stone and Brooks, 1990; Frank and Friedman, 1993).
Since it uses the response \(\mathbf{y}\) to construct its directions, its solution path is a nonlinear function of \(\mathbf{y}\).
In particular, the \(m\)th principal component direction \(v_m\) solves:
\begin{equation*} \max_\alpha \text{Var}(\mathbf{X}\alpha)\\ \text{subject to } \|\alpha\| = 1, \alpha^T\mathbf{S} v_l = 0 \text{ for } l = 1,\cdots, m-1, \end{equation*}
where \(\mathbf{S}\) is the sample covariance matrix of the \(\mathbf{x}_j\). The condition \(\alpha^T\mathbf{S} v_l= 0\) ensures that \(\mathbf{z}_m = \mathbf{X}\alpha\) is uncorrelated with all the previous linear combinations \(\mathbf{z}_l = \mathbf{X} v_l\).
The \(m\)th PLS direction \(\hat\rho_m\) solves:
\begin{equation*} \max_\alpha \text{Corr}^2(\mathbf{y},\mathbf{S}\alpha)\text{Var}(\mathbf{X}\alpha)\\ \text{subject to } \|\alpha\| = 1, \alpha^T\mathbf{S}\hat\rho_l = 0 \text{ for } l=1,\cdots, m-1. \end{equation*}
Further analysis reveals that the variance aspect tends to dominate, and so PLS behaves much like ridge regression and PCR.
Partial least squares also tends to shrink the low-variance directions, but can actually inflate some of the higher variance directions. This can make PLS a little unstable, and cause it to have slightly higher prediction error compared to ridge regression.
PLS, PCR and ridge regression tend to behave similarly. Ridge regression may be preferred because it shrinks smoothly, rather than in discrete steps. Lasso falls somewhere between ridge regression and best subset regression, and enjoys some of the properties of each.
Example: Prostate Cancer¶
The data for this example come from a study by Stamey et al. (1989) that examined the correlation between the level of prostate specific antigen (PSA) and a number of clinical measures, in 97 men who were about to receive a radical prostatectomy. The goal is to predict the log of PSA (lpsa) from a number of measurements.
The data has variables:
lpsa: log prostate specific antigen
lcavol: log cancer volume
lweight: log prostate weight
age: age
lbph: log of benign prostatic hyperplasia amount
svi: seminal vesicle invasion
lcp: log of capsular penetration
gleason: Gleason score
pgg45: percent of Gleason scores 4 or 5
We split data to training and test data.
[23]:
ORANGE, BLUE, PURPLE = '#E69F00', '#56B4E9', '#A020F0'
GRAY1, GRAY4 = '#231F20', '#646369'
target = 'lpsa'
features = ['lcavol', 'lweight', 'age', 'lbph', 'svi', 'lcp', 'gleason', 'pgg45']
df = pd.read_csv(data_path + "prostate_cancer.txt")
display(df.head())
sns.pairplot(df, vars=[target]+features, kind="scatter", height=1.1)
# split data to training/test np.arrays
is_train = df.train == 'T'
X, y = df[features].values, df[target].values
X_train, y_train = X[is_train], y[is_train]
X_test, y_test = X[~is_train], y[~is_train]
N_test = len(y_test)
display(df[is_train][features].corr())
toggle()
| id | lcavol | lweight | age | lbph | svi | lcp | gleason | pgg45 | lpsa | train | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | -0.579818 | 2.769459 | 50 | -1.386294 | 0 | -1.386294 | 6 | 0 | -0.430783 | T |
| 1 | 2 | -0.994252 | 3.319626 | 58 | -1.386294 | 0 | -1.386294 | 6 | 0 | -0.162519 | T |
| 2 | 3 | -0.510826 | 2.691243 | 74 | -1.386294 | 0 | -1.386294 | 7 | 20 | -0.162519 | T |
| 3 | 4 | -1.203973 | 3.282789 | 58 | -1.386294 | 0 | -1.386294 | 6 | 0 | -0.162519 | T |
| 4 | 5 | 0.751416 | 3.432373 | 62 | -1.386294 | 0 | -1.386294 | 6 | 0 | 0.371564 | T |
| lcavol | lweight | age | lbph | svi | lcp | gleason | pgg45 | |
|---|---|---|---|---|---|---|---|---|
| lcavol | 1.000000 | 0.300232 | 0.286324 | 0.063168 | 0.592949 | 0.692043 | 0.426414 | 0.483161 |
| lweight | 0.300232 | 1.000000 | 0.316723 | 0.437042 | 0.181054 | 0.156829 | 0.023558 | 0.074166 |
| age | 0.286324 | 0.316723 | 1.000000 | 0.287346 | 0.128902 | 0.172951 | 0.365915 | 0.275806 |
| lbph | 0.063168 | 0.437042 | 0.287346 | 1.000000 | -0.139147 | -0.088535 | 0.032992 | -0.030404 |
| svi | 0.592949 | 0.181054 | 0.128902 | -0.139147 | 1.000000 | 0.671240 | 0.306875 | 0.481358 |
| lcp | 0.692043 | 0.156829 | 0.172951 | -0.088535 | 0.671240 | 1.000000 | 0.476437 | 0.662533 |
| gleason | 0.426414 | 0.023558 | 0.365915 | 0.032992 | 0.306875 | 0.476437 | 1.000000 | 0.757056 |
| pgg45 | 0.483161 | 0.074166 | 0.275806 | -0.030404 | 0.481358 | 0.662533 | 0.757056 | 1.000000 |
[23]:

The baseline prediction is using the mean of the training set.
[24]:
from sklearn.dummy import DummyRegressor
from sklearn.metrics import mean_squared_error
null_model = DummyRegressor().fit(X_train, y_train)
base_error_rate = mean_squared_error(y_test, null_model.predict(X_test))
print(f'Baseline Test Error: {base_error_rate:.3f}')
Baseline Test Error: 1.057
We exhaustively search over specified parameter values for an estimator. The least complex model within one standard error of the best is chosen. The grid search object has 10-fold cross validation. Three functions, cross_validation, assess_selected_model and plot_cv_results, are built for our testing.
[25]:
from sklearn.model_selection import GridSearchCV, KFold
def cross_validation(estimator, param_grid):
# prepare grid search object with 10-fold cross validation it uses
# neg_mean_squared_error due to the higher is the better approach
K=10
grid_search = GridSearchCV(
estimator, param_grid, cv=KFold(K, True, 69438),
scoring='neg_mean_squared_error', return_train_score=True, iid=True
).fit(X_train, y_train)
# convert neg_mean_squared_error to mean squared error and reshape results
# to the form where a row correspons to one paramenter's 10 cross
# validation mse values
cv_erros = -np.vstack([grid_search.cv_results_[f'split{i}_test_score']
for i in range(K)]).T
# calculate mean squared error for parameters and their standard error
cv_mean_errors = np.mean(cv_erros, axis=1)
cv_std_errors = np.std(cv_erros, ddof=1, axis=1)/np.sqrt(K)
# The least complex model within one standard error of the best is chosen
best_index = np.argmin(cv_mean_errors)
best_err = cv_mean_errors[best_index]
best_std_err = cv_std_errors[best_index]
model_index = np.argmax(cv_mean_errors < (best_err+best_std_err))
return cv_mean_errors, cv_std_errors, best_err, best_std_err, model_index
# calculates the estimator's test mean squared error and its standard error
def assess_selected_model(estimator):
y_hat = np.squeeze(estimator.predict(X_test))
error_rate = mean_squared_error(y_test, y_hat)
std_error = np.std((y_test - y_hat)**2, ddof=1)/np.sqrt(N_test)
return error_rate, std_error
def plot_cv_results(title, x_label, test_error, std_error, complexity_vals,
cv_mean_errors, cv_std_errors, best_err, best_std_err,
selected_model_index):
fig, ax = plt.subplots(figsize=(4, 3.1), dpi=110)
ax.plot(complexity_vals, cv_mean_errors, c=ORANGE, linewidth=0.8)
ax.errorbar(
complexity_vals, cv_mean_errors, color=ORANGE, linestyle='None',
marker='o', elinewidth=0.8, markersize=3, yerr=cv_std_errors,
ecolor=BLUE, capsize=3)
ax.axhline(y=best_err+best_std_err, c=PURPLE, linewidth=0.8,
linestyle='--')
ax.axvline(x=complexity_vals[selected_model_index], c=PURPLE,
linewidth=0.8, linestyle='--')
for i in ax.get_yticklabels() + ax.get_xticklabels():
i.set_fontsize(6)
ax.text(ax.get_xlim()[0], 1.85, title, color=GRAY4, fontsize=9)
ax.set_xlabel(x_label, color=GRAY4, fontsize=8)
ax.set_ylabel('CV Error', color=GRAY4, fontsize=8)
parms = {'color': GRAY1, 'fontsize': 7,
'bbox': {'facecolor': 'white', 'pad': 0, 'edgecolor': 'none'}}
lim = ax.get_xlim()
text_x = lim[1] - (lim[1]-lim[0])*0.02
ax.text(
text_x, 1.72, f'Test Error: {test_error:.3f}', **parms, ha='right')
ax.text(text_x, 1.63, f' Std Error: {std_error:.3f}', **parms, ha='right')
toggle()
[25]:
Least Square¶
[26]:
from sklearn.preprocessing import StandardScaler
import statsmodels.api as sm
scaler = StandardScaler().fit(X)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
ls = sm.OLS(y_train, sm.add_constant(X_train)).fit()
ls_params = ls.params
display(ls.summary())
y_hat = ls.predict(sm.add_constant(X_test))
ls_error_rate = mean_squared_error(y_test, y_hat)
ls_std_error = np.std((y_test - y_hat)**2, ddof=1)/np.sqrt(N_test)
print(f'Least Squares Test Error: {ls_error_rate:.3f}')
print(f' Std Error: {ls_std_error:.3f}')
toggle()
| Dep. Variable: | y | R-squared: | 0.694 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.652 |
| Method: | Least Squares | F-statistic: | 16.47 |
| Date: | Thu, 10 Oct 2019 | Prob (F-statistic): | 2.04e-12 |
| Time: | 20:12:15 | Log-Likelihood: | -67.505 |
| No. Observations: | 67 | AIC: | 153.0 |
| Df Residuals: | 58 | BIC: | 172.9 |
| Df Model: | 8 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 2.4649 | 0.089 | 27.598 | 0.000 | 2.286 | 2.644 |
| x1 | 0.6760 | 0.126 | 5.366 | 0.000 | 0.424 | 0.928 |
| x2 | 0.2617 | 0.095 | 2.751 | 0.008 | 0.071 | 0.452 |
| x3 | -0.1407 | 0.101 | -1.396 | 0.168 | -0.343 | 0.061 |
| x4 | 0.2091 | 0.102 | 2.056 | 0.044 | 0.006 | 0.413 |
| x5 | 0.3036 | 0.123 | 2.469 | 0.017 | 0.057 | 0.550 |
| x6 | -0.2870 | 0.154 | -1.867 | 0.067 | -0.595 | 0.021 |
| x7 | -0.0212 | 0.144 | -0.147 | 0.884 | -0.310 | 0.268 |
| x8 | 0.2656 | 0.153 | 1.738 | 0.088 | -0.040 | 0.571 |
| Omnibus: | 0.825 | Durbin-Watson: | 1.690 |
|---|---|---|---|
| Prob(Omnibus): | 0.662 | Jarque-Bera (JB): | 0.389 |
| Skew: | -0.164 | Prob(JB): | 0.823 |
| Kurtosis: | 3.178 | Cond. No. | 4.47 |
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Least Squares Test Error: 0.521
Std Error: 0.179
[26]:
Ridge Regression¶
[27]:
from sklearn.linear_model import Ridge
degress_of_freedom = list(range(9))
# these alpha parameters correspond to 0-8 degrees of freedom
parameters = {'alpha': [1e20, 436, 165, 82, 44, 27, 12, 4, 1e-05]}
rd_errs, rd_std_errs, best_err, best_std_err, selected_index = \
cross_validation(Ridge(), parameters)
rd = Ridge(alpha=parameters['alpha'][selected_index]).fit(X_train, y_train)
rd_params = np.hstack((rd.intercept_, rd.coef_))
rd_error_rate, rd_std_error = assess_selected_model(rd)
plot_cv_results(
'Ridge Regression', 'Degrees of Freedom', rd_error_rate, rd_std_error,
degress_of_freedom, rd_errs, rd_std_errs, best_err, best_std_err,
selected_index)
toggle()
[27]:
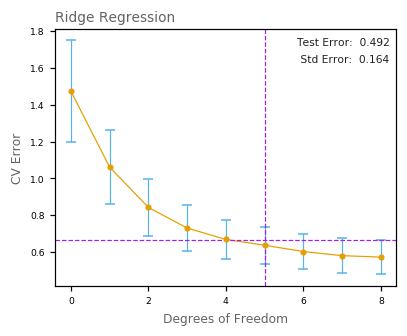
Lasso Regression¶
[28]:
from sklearn.linear_model import Lasso
shrinkage = [0, 0.102, 0.254, 0.384, 0.504, 0.612, 0.756, 0.883, 1]
# these alpha parameters correspond to above shrinkage values
parameters = {
'alpha': [1, 0.680, 0.380, 0.209, 0.100, 0.044, 0.027, 0.012, 0.001]}
lo_errs, lo_std_errs, best_err, best_std_err, selected_index = \
cross_validation(Lasso(), parameters)
lo = Lasso(alpha=parameters['alpha'][selected_index]).fit(X_train, y_train)
lo_params = np.hstack((lo.intercept_, lo.coef_))
lo_error_rate, lo_std_error = assess_selected_model(lo)
plot_cv_results(
'Lasso', 'Shrinkage Factor s', lo_error_rate, lo_std_error, shrinkage,
lo_errs, lo_std_errs, best_err, best_std_err, selected_index)
toggle()
[28]:
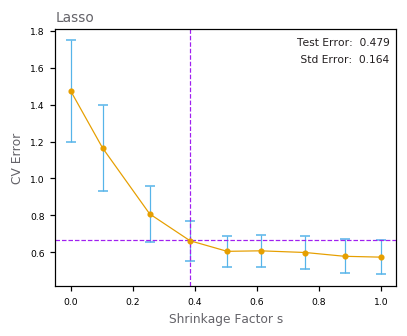
Best Subset Regression¶
[29]:
from itertools import combinations
class BestSubsetRegression(LinearRegression):
def __init__(self, subset_size=1):
LinearRegression.__init__(self)
self.subset_size = subset_size
def fit(self, X, y, sample_weight=None):
best_combination, best_mse = None, None
best_intercept_, best_coef_ = None, None
# try all combinations of subset_size
for combination in combinations(range(X.shape[1]), self.subset_size):
X_tmp = X[:, combination]
LinearRegression.fit(self, X_tmp, y)
mse = mean_squared_error(y, self.predict(X_tmp))
if best_mse is None or best_mse > mse:
# select the best combination
best_combination, best_mse = combination, mse
best_intercept_, best_coef_ = self.intercept_, self.coef_
LinearRegression.fit(self, X, y)
# replace intercept and parameters with the found, set other zero
self.intercept_ = best_intercept_
self.coef_ = np.zeros(shape=self.coef_.shape)
for i, idx in enumerate(best_combination):
self.coef_[idx] = best_coef_[i]
return self
# it is not possible to use Best Subset with 0 size, so run CV with 1-8 k
parameters = {'subset_size': list(range(1, 9))}
# run CV to chose best parameter
bs_errs, bs_std_errs, best_err, best_std_err, selected_index = \
cross_validation(BestSubsetRegression(), parameters)
bs = BestSubsetRegression(subset_size=parameters['subset_size'][selected_index]).fit(X_train, y_train)
bs_params = np.hstack((bs.intercept_, bs.coef_))
bs_error_rate, bs_std_error = assess_selected_model(bs)
subset_sizes = list(range(0, 9))
plot_cv_results(
'All Subsets', 'Subset Size', bs_error_rate, bs_std_error, subset_sizes,
np.hstack((lo_errs[0], bs_errs)), np.hstack((lo_std_errs[0], bs_std_errs)),
best_err, best_std_err, selected_index+1)
toggle()
[29]:
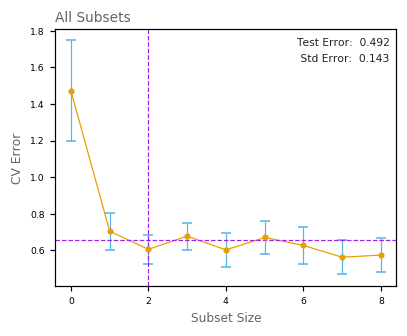
Principal Components Regression¶
[30]:
from sklearn.decomposition import PCA
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LinearRegression
n_directions = list(range(0, 9))
# it is not possible to use PCA with 0 directions, so run CV with 1-8 directions
parameters = {'pca__n_components': list(range(1, 9))}
model = Pipeline([('pca', PCA()),
('regression', LinearRegression())])
pc_errs, pc_std_errs, best_err, best_std_err, selected_index = \
cross_validation(model, parameters)
# refit the model to the training set with n-directions from CV
pca = PCA(n_components=parameters['pca__n_components'][selected_index])
lr = LinearRegression()
model = Pipeline([('pca', pca),
('regression', lr)]).fit(X_train, y_train)
# X_train are not centered, so calculation is little bit different
pc_params = np.zeros(8)
intercept = lr.intercept_
for i in range(7):
pc_params += lr.coef_[i]*pca.components_[i, :]
intercept -= lr.coef_[i]*(pca.mean_ @ pca.components_[i, :])
pc_params = np.hstack(([intercept], pc_params))
pc_error_rate, pc_std_error = assess_selected_model(model)
plot_cv_results(
'Principal Components Regression', 'Number of Directions', pc_error_rate,
pc_std_error, n_directions, np.hstack((lo_errs[0], pc_errs)),
np.hstack((lo_std_errs[0], pc_std_errs)), best_err, best_std_err,
selected_index+1)
toggle()
[30]:
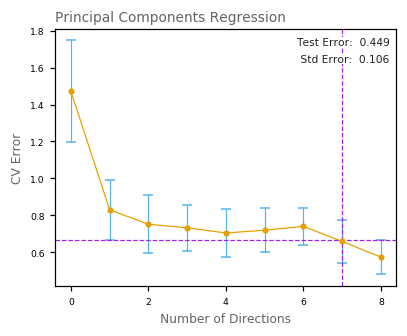
Partial Least Squares¶
[31]:
from sklearn.cross_decomposition import PLSRegression
parameters = {'n_components': list(range(1, 9))}
ps_errs, ps_std_errs, best_err, best_std_err, selected_index = \
cross_validation(PLSRegression(scale=False), parameters)
# out cross-validation gives 3 components, but let's pretend that the result is
# n = 2 components to be consistent with the book
ps = PLSRegression(n_components=2, scale=False).fit(X_train, y_train)
ps_params = np.hstack((ps.y_mean_, np.squeeze(ps.coef_)))
ps_error_rate, ps_std_error = assess_selected_model(ps)
n_directions = list(range(0, 9))
plot_cv_results(
'Partial Least Squares', 'Number of Directions', ps_error_rate,
ps_std_error, n_directions, np.hstack((lo_errs[0], ps_errs)),
np.hstack((lo_std_errs[0], ps_std_errs)), best_err, best_std_err,
selected_index+1)
toggle()
[31]:
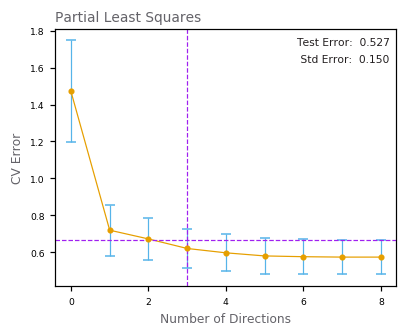
[32]:
result = zip(['Intercept'] + features,
ls_params, bs_params, rd_params, lo_params, pc_params, ps_params)
print(' Term LS Best Subset Ridge Lasso PCR PLS')
print('---------------------------------------------------------------------')
for term, ls, bs, rd, lo, pc, ps in result:
print(f'{term:>10}{ls:>9.3f}{bs:>14.3f}{rd:>9.3f}{lo:>9.3f}{pc:>9.3f}'
f'{ps:>9.3f}')
print('---------------------------------------------------------------------')
print(f'Test Error{ls_error_rate:>9.3f}{bs_error_rate:>14.3f}'
f'{rd_error_rate:>9.3f}{lo_error_rate:>9.3f}{pc_error_rate:>9.3f}'
f'{ps_error_rate:>9.3f}')
print(f' Std Error{ls_std_error:>9.3f}{bs_std_error:>14.3f}'
f'{rd_std_error:>9.3f}{lo_std_error:>9.3f}{pc_std_error:>9.3f}'
f'{ps_std_error:>9.3f}')
toggle()
Term LS Best Subset Ridge Lasso PCR PLS
---------------------------------------------------------------------
Intercept 2.465 2.477 2.464 2.468 2.497 2.452
lcavol 0.676 0.736 0.405 0.536 0.548 0.417
lweight 0.262 0.315 0.234 0.187 0.287 0.343
age -0.141 0.000 -0.042 0.000 -0.154 -0.026
lbph 0.209 0.000 0.158 0.000 0.213 0.219
svi 0.304 0.000 0.221 0.085 0.313 0.242
lcp -0.287 0.000 0.010 0.000 -0.062 0.078
gleason -0.021 0.000 0.042 0.000 0.226 0.011
pgg45 0.266 0.000 0.128 0.006 -0.048 0.083
---------------------------------------------------------------------
Test Error 0.521 0.492 0.492 0.479 0.449 0.527
Std Error 0.179 0.143 0.164 0.164 0.106 0.150
[32]:
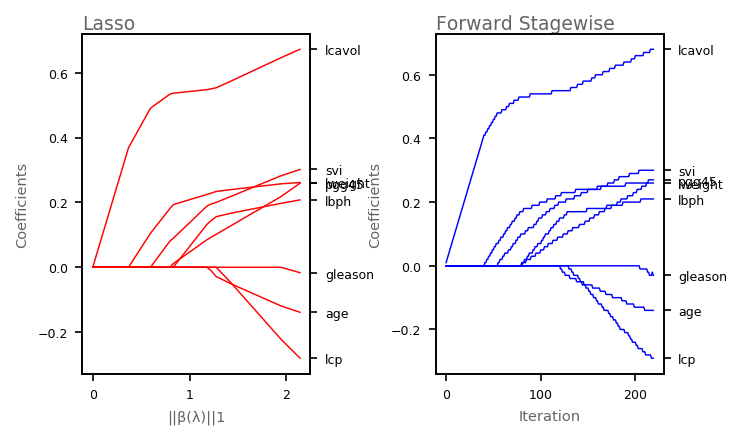
Forward Stagewise Regression¶
The plot shows the profiles of estimated coefficients from linear regression. The left panel shows the results from the lasso, for different values of the bound parameter \(t = \sum_k |\alpha_k|\). The right panel shows the results of the stagewise linear regression, using \(M = 220\) consecutive steps of size \(\epsilon = .01\).
[33]:
alpha = np.linspace(0.001, 0.93, 100)
b_hat = np.vstack([Lasso(alpha=a).fit(X_train, y_train).coef_
for a in reversed(alpha)])
b_pow = np.sum(np.abs(b_hat), axis=1)
# Forward Stagewise Linear Regression
scaler = StandardScaler(with_std=False)
y_train_scaled = np.squeeze(scaler.fit_transform(np.atleast_2d(y_train).T))
eps, K, M = 0.01, X_train.shape[1], 220
a_hat = None
a_hat_current = np.zeros(shape=(K))
for m in range(M):
resid = y_train_scaled - X_train @ a_hat_current
best_sum_squares, b_star, k_star = None, None, None
for k in range(K):
X_train_k = X_train[:, k:k+1]
lstsq_result = np.linalg.lstsq(X_train_k, resid)
b, sum_squares = lstsq_result[0], lstsq_result[1][0]
if best_sum_squares is None or best_sum_squares > sum_squares:
best_sum_squares, b_star, k_star = sum_squares, b, k
a_hat_current[k_star] += eps * np.sign(b_star)[0]
if a_hat is None:
a_hat = np.copy(a_hat_current)
else:
a_hat = np.vstack((a_hat, a_hat_current))
def plot_coef_profiles(ax, title, color, coef, x_values, x_title):
for i in range(coef.shape[1]):
ax.plot(x_values, coef[:, i], color=color, linewidth=0.7)
ax2 = ax.twinx()
ax2.set_ylim(ax.get_ylim())
plt.setp(ax2, yticks=coef[-1], yticklabels=features)
for i in ax.get_yticklabels() + ax.get_xticklabels() + \
ax2.get_yticklabels():
i.set_fontsize(6)
ax.set_xlabel(x_title, color=GRAY4, fontsize=7)
ax.set_ylabel('Coefficients', color=GRAY4, fontsize=7)
ax.text(ax.get_xlim()[0], ax.get_ylim()[1]*1.02, title, color=GRAY4,
fontsize=9)
fig, axarr = plt.subplots(1, 2, figsize=(5, 3), dpi=150)
plt.subplots_adjust(wspace=0.55)
plot_coef_profiles(axarr[0], 'Lasso', 'red', b_hat, b_pow, '||β(λ)||1')
plot_coef_profiles(axarr[1], 'Forward Stagewise', 'blue', a_hat, range(M),
'Iteration')
toggle()
[33]:
Basis Functions¶
The basis expansions are a general means to achieve more flexible representations for \(f(\mathbf{x}, \mathbf{w})\). Nonlinear basis functions allows the function \(f(\mathbf{x}, \mathbf{w})\) to be a nonlinear function of the input vector \(\mathbf{x}\). However, since the model is still liner in \(\mathbf{w}\), the analysis is still simple for this class of model.
Piecewise Polynomials and Splines¶
Polynomials are typical functions used for basis expansions. One limitation of polynomial basis functions is their global nature that tweaking the coefficients to improve the fitting in one region can cause the function flap about madly in remote region.
spline functions are used to resolved the issue by dividing the input space up into regions and fit a different polynomial in each region with certain continuity requirements at connection points called knots. For example, cubic spline is continuous and has continuous first and second derivatives.
regression splines are splines with fixed knots.
However, polynomial fitting tends to be erratic near the boundaries. Nature cubic spline poses an additional requirement that the function is linear beyond the boundary knots.
A natural cubic spline with \(K\) knots is represented by \(K\) basis functions. For example:
\begin{align*} N_1(x) = 1, N_2(x) = x, N_{k+2} = \frac{(x-\xi_k)^3_+}{\xi_K - \xi_k} - \frac{(x-\xi_{K-1})^3_+}{\xi_K - \xi_{K-1}} \end{align*}
where \(\xi_1, \ldots, \xi_K\) are knots.
A retrospective sample of males in a heart-disease high-risk region of the Western Cape, South Africa.
variable |
description |
|---|---|
sbp |
systolic blood pressure |
tobacco |
cumulative tobacco (kg) |
ldl |
low densiity lipoprotein cholesterol |
adiposity |
|
famhist |
family history of heart disease (Present, Absent) |
typea |
type-A behavior |
obesity |
|
alcohol |
current alcohol consumption |
age |
age at onset |
chd |
response, coronary heart disease |
[34]:
import statsmodels.api as sm
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import FunctionTransformer
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import log_loss
df = pd.read_csv(data_path + "south_african_heart_disease.txt")
df['famhist'] = pd.get_dummies(df['famhist'])['Present']
target = ['chd']
features = ['sbp', 'tobacco', 'ldl', 'famhist', 'obesity', 'age']
df.head()
X, y = df[features].values, np.squeeze(df[target].values)
class NaturalCubicSplineFeatures():
# you can specify knots locations or degrees of freedom
def __init__(self, knots=None, df=None):
self.knots = knots
self.df = df
@staticmethod
def dk(x, xi_k, xi_K):
return (max(0, x-xi_k)**3) / (xi_K-xi_k)
@staticmethod
def natural_cubic_expansion(x, xis):
X = np.zeros(shape=(x.shape[0], len(xis)-1))
for i in range(X.shape[0]):
X[i, 0] = x[i]
for k in range(2, len(xis)):
dk1 = NaturalCubicSplineFeatures.dk(x[i], xis[k-2], xis[-1])
dk2 = NaturalCubicSplineFeatures.dk(x[i], xis[-2], xis[-1])
X[i, k-1] = dk1 - dk2
return X
def fit(self, X, y=None):
if self.df is not None:
quantiles = np.linspace(0, 1, self.df+1)
self.knots = []
for i in range(X.shape[1]):
self.knots.append(np.unique(np.quantile(X[:, i], quantiles)))
# calculate the number of parameters in each component term
self.dofs_ = np.array([len(k)-1 for k in self.knots])
pts = [0] + list(np.cumsum(self.dofs_))
self.pos_ = [(pts[i-1], pts[i]-1) for i in range(1, len(pts))]
return self
def transform(self, X):
h = []
for i in range(X.shape[1]):
h.append(NaturalCubicSplineFeatures.natural_cubic_expansion(
X[:, i], self.knots[i]))
result = np.hstack(h)
return result
ncs = NaturalCubicSplineFeatures(df=4)
add_intercept = FunctionTransformer(
lambda X: sm.add_constant(X), validate=True)
prep = Pipeline([('scale_features', StandardScaler()),
('expand_basis', ncs),
('scale_basis', StandardScaler()),
('add_intercept_column', add_intercept)])
X_min, X_max = np.min(X, axis=0), np.max(X, axis=0)
lr = LogisticRegression(solver='lbfgs', max_iter=100000, C=10e10, fit_intercept=False)
model = Pipeline([('prepare', prep),
('logistic', lr)])
model.fit(X, y);
H = prep.transform(X)
predProbs = model.predict_proba(X)
W = np.diagflat(np.product(predProbs, axis=1))
cov = np.linalg.inv(H.T @ W @ H)
x_axis_values = np.vstack([np.linspace(X_min[i], X_max[i], 100)
for i in range(X_min.shape[0])]).T
x_axis_values_ = prep.transform(x_axis_values)
def plot_term_natural_spline_function(ax, feature_i, name):
basis_start, basis_end = ncs.pos_[feature_i]
basis_start += 1
basis_end += 1
feature_basis = x_axis_values_[:, basis_start:basis_end+1]
feature_cov = cov[basis_start:basis_end+1, basis_start:basis_end+1]
err = [2*np.sqrt(feature_basis[t:t+1, :] @
feature_cov @ feature_basis[t:t+1, :].T)[0, 0]
for t in range(100)]
err = np.array(err)
x_values = x_axis_values[:, feature_i]
y_values = np.squeeze(
feature_basis @ lr.coef_[:, basis_start:basis_end+1].T)
y_values_low = y_values - err
y_values_high = y_values + err
ax.fill_between(x_values, y_values_low, y_values_high, color='#FFEC8B')
ax.plot(x_values, y_values, color='#00FF00', linewidth=0.8)
y_from, y_to = ax.get_ylim()
for i in range(X.shape[0]):
x = X[i, feature_i]
ax.plot([x, x], [y_from, y_from+(y_to-y_from)*0.02],
color='red', linewidth=0.5)
ax.set_ylim(y_from, y_to)
for l in ax.get_yticklabels() + ax.get_xticklabels():
l.set_fontsize(6)
ax.set_xlabel(f'{name}', color=GRAY4, fontsize=8)
ax.set_ylabel(f'f({name})', color=GRAY4, fontsize=8)
fig, axes = plt.subplots(3, 2, figsize=(3.3*2, 2.3*3), dpi=150)
plt.subplots_adjust(bottom=-0.05)
plot_term_natural_spline_function(axes[0, 0], 0, 'sbp')
plot_term_natural_spline_function(axes[0, 1], 1, 'tobacco')
plot_term_natural_spline_function(axes[1, 0], 2, 'ldl')
plot_term_natural_spline_function(axes[1, 1], 3, 'famhist')
plot_term_natural_spline_function(axes[2, 0], 4, 'obesity')
plot_term_natural_spline_function(axes[2, 1], 5, 'age')
toggle()
[34]:
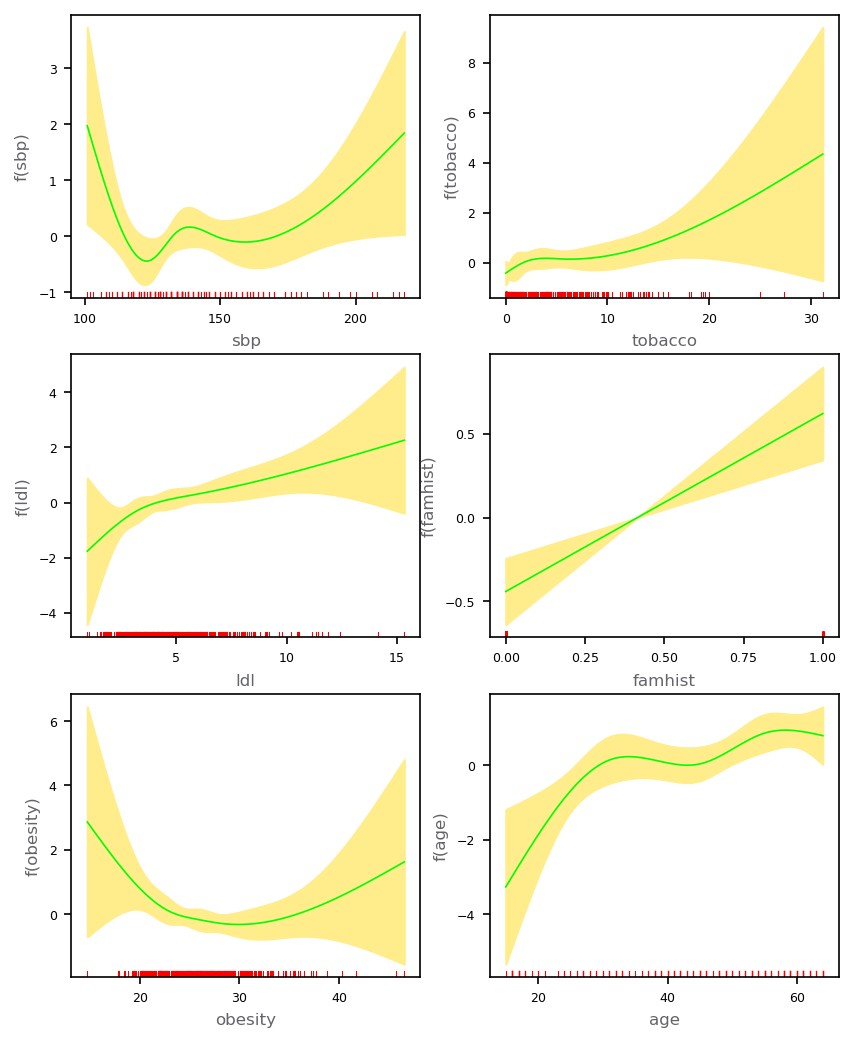
The plot has fitted natural-spline functions for each of the terms in the model with selected independent variables with pointwise standard-error bands. The rug plot at the base of each figure indicates the location of each of the sample values for that variable.
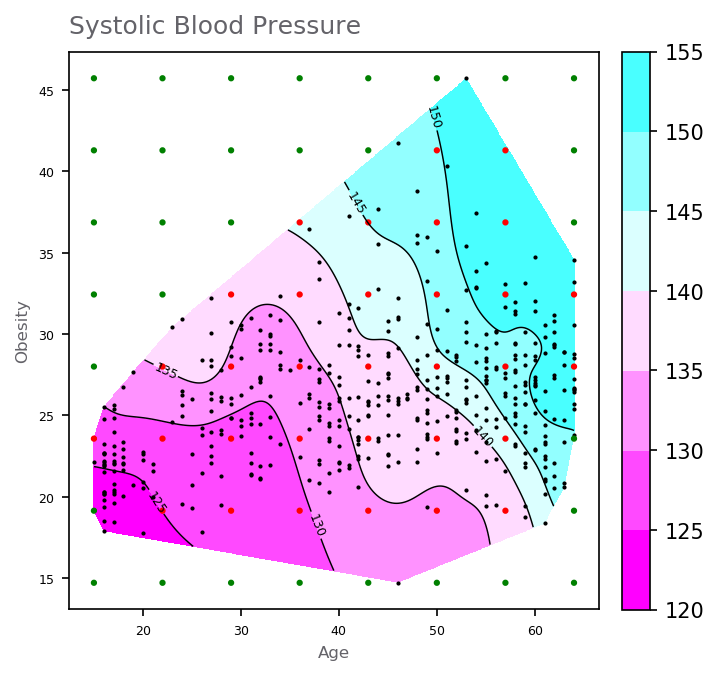
Smoothing Splines¶
For one-dimensional inputs, consider the problem of finding a function \(f(x)\) with two continuous derivatives that minimize the penalized residual sum of squares
\begin{align*} RSS(f, \lambda) = \sum_{i=1}^{n} (y_i - f(x_i))^2 + \lambda \int (f^{\prime \prime}(t))^2 dt \end{align*}
\(\lambda = 0\): \(f\) can be any function that interpolates the data
\(\lambda = \infty\): the simple least squares line fit
We can show that nature cubic spline with knots at \(x_1, \ldots, x_n\) is the unique minimizer.
[35]:
from scipy.spatial import ConvexHull
from scipy.interpolate import Rbf
from matplotlib import cm
# checks whether a point is inside a convex hull
def point_in_hull(point, hull, tolerance=1e-12):
return all((np.dot(eq[:-1], point) + eq[-1] <= tolerance)
for eq in hull.equations)
# remove 1 outlier because it greatly expands the convex hull
df1 = df[~((df.age < 20) & (df.obesity > 45))]
x, y, z = df1.age.values, df1.obesity.values, df1.sbp.values
# don't know why, but relocating response influences on approximation
# scaling does no have any effect
mean_z = np.mean(z)
z = z - mean_z
# build a convex hull
xy = np.vstack((x, y)).T
hull = ConvexHull(xy)
# calculate approximation on whole x-y range
xi, yi = np.meshgrid(np.linspace(np.min(x), np.max(x), 500),
np.linspace(np.min(y), np.max(y), 500))
rbfi = Rbf(x, y, z, smooth=30, function='multiquadric')
zi = rbfi(xi, yi)
# remove all points outside the convex hull
for i in range(xi.shape[0]):
for j in range(xi.shape[1]):
if not point_in_hull([xi[i, j], yi[i, j]], hull):
zi[i, j] = None
levels = [120, 125, 130, 135, 140, 145, 150, 155]
colors = ['#FF00FF', '#FF49FF', '#FF92FF', '#FFDBFF',
'#DBFFFF', '#92FFFF', '#49FFFF', '#00FFFF']
fig, ax = plt.subplots(figsize=(5, 5), dpi=150)
cf = ax.contourf(xi, yi, zi+mean_z, levels=levels, colors=colors)
cs = ax.contour(
xi, yi, zi+mean_z, levels=levels, colors='black', linewidths=0.7)
ax.clabel(cs, inline=1, fontsize=6, fmt='%1.0f')
ax.scatter(x, y, s=1, color='black')
ax.set_aspect(1.66)
x_vals = np.linspace(15, 64, 8)
y_vals = np.linspace(14.7, 45.72, 8)
latice = np.transpose([np.tile(x_vals, 8), np.repeat(y_vals, 8)])
colors = [('green', 'red')[point_in_hull(latice[i], hull)]
for i in range(latice.shape[0])]
ax.scatter(latice[:, 0], latice[:, 1], s=4, color=colors)
for l in ax.get_yticklabels() + ax.get_xticklabels():
l.set_fontsize(6)
ax.set_xlabel('Age', color=GRAY4, fontsize=8)
ax.set_ylabel('Obesity', color=GRAY4, fontsize=8)
fig.colorbar(cf, ax=ax, fraction=0.048, pad=0.04)
_ = ax.text(12.5, 48.5, 'Systolic Blood Pressure', color=GRAY4, fontsize=12)
toggle()
[35]:
There are many other possible choices of basis functions, such as Gaussian basis function
\begin{align} \phi_j (x) = \exp \left\{ - \frac{(x-\mu_j)^2}{2s^2} \right\} \nonumber \end{align}
and Sigmoidal basis function
\begin{align} \phi_j (x) = \sigma \left( \frac{x-\mu_j}{s} \right) \text{ with } \sigma(z) = \frac{1}{1+\exp(-z)} \nonumber \end{align}
where \(\mu_j\) govern the locations of the basis function in input space, and the parameter \(s\) governs their spatial scale.
We plot basis functions, including polynomials, Gaussians, and Sigmoidals, as follows.
[36]:
x = np.linspace(-1, 1, 100)
funcs = {'Polynomial': [11], 'Gaussian': [np.linspace(-1, 1, 11), 0.1],'Sigmoidal': [np.linspace(-1, 1, 11), 10]}
# call polynomial(11).dm(x), gaussian(-1,1,11).dm(x) etc.
# phi = [globals()[key.lower()](*value).dm(x) for key, value in funcs.items()]
phi = [globals()[key](*value).dm(x) for key, value in funcs.items()]
plt.figure(figsize=(15, 4))
for i, X in enumerate(phi):
plt.subplot(1, 3, i + 1)
for j in range(12):
plt.plot(x, X[:, j])
toggle()
[36]:
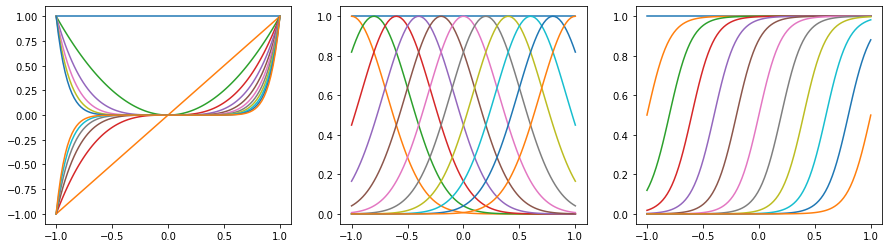
The first plot has constant, linear, quadratic functions and so on.
The second plot shows a group of shifting normal density curves.
The third plot shows a group of shifting logistic sigmoid functions.
Bayesian Regression¶
We assume that the target variable \(y\) is given by \(f(\mathbf{x}, \mathbf{w})\) with additive Gaussian noise with precision \(\beta\), which is \(y = f(\mathbf{x}, \mathbf{w}) + \epsilon\). The approach defines a generative model
\begin{align*} p(y|\mathbf{x},\mathbf{w}, \beta) &= \mathcal{N}(y|f(\mathbf{x},\mathbf{w}), \beta^{-1}) \label{prob_dist_target} \end{align*}
Maximal Likelihood¶
The log likelihood function is
\begin{align} \ln p(\mathbf{y}|\mathbf{X},\mathbf{w}, \beta) & = \frac{N}{2} \ln \beta - \frac{N}{2} \ln(2\pi) - \beta \textrm{E}_{\mathcal{D}}(\mathbf{w})\nonumber \end{align}
where \begin{align*} \textrm{E}_{\mathcal{D}}(\mathbf{w}) = \sum_{i=1}^{n}\left( y_i - \mathbf{w}^\intercal \phi(\mathbf{x}_{i}) \right)^2 = \text{RSS}(\mathbf{w}) \end{align*}
So
\begin{align*} \max ~\ln p(\mathbf{y}|\mathbf{X},\mathbf{w}, \beta) \text{ is equivalent to } \min~\text{RSS}(\mathbf{w}) \end{align*}
[37]:
hide_comment()
[37]:
Note that
\begin{align} p(y|\mathbf{x},\mathbf{w}, \beta) &= \mathcal{N}(y|f(\mathbf{x},\mathbf{w}), \beta^{-1}) = \mathcal{N}(y|\mathbf{w}^\intercal \phi(\mathbf{x}), \beta^{-1}) \nonumber \end{align}
The likelihood function is
\begin{align} p(\mathbf{y}|\mathbf{X},\mathbf{w}, \beta) &= \prod_{i=1}^{n} \mathcal{N}(y_i|\mathbf{w}^\intercal \phi(\mathbf{x}_{i}), \beta^{-1}) \nonumber \\ &= \prod_{i=1}^{n} \frac{\beta^{1/2}}{(2\pi)^{1/2}} \exp\left( \frac{\beta}{2} (y_i - \mathbf{w}^\intercal \phi(\mathbf{x}_{i}))^2 \right) \label{likelihood} \end{align}
The log likelihood function is
\begin{align} \ln p(\mathbf{t}|\mathbf{X},\mathbf{w}, \beta) &= \frac{n}{2} \ln \beta - \frac{n}{2} \ln(2\pi) - \frac{\beta}{2} \sum_{i=1}^{n}\left( y_i - \mathbf{w}^\intercal \phi(\mathbf{x}_{i}) \right)^2 \nonumber \\ & \equiv \frac{n}{2} \ln \beta - \frac{n}{2} \ln(2\pi) - \beta E_{\mathcal{D}}(\mathbf{w})\nonumber \end{align}
\(\blacksquare\)
Regularization¶
We can view regularization as Bayesian estimates. Suppose the noise precision parameter \(\beta\) is known. The likelihood function is. Note that the inputs \(\mathbf{x}\) will always appear in the set of conditioning variables. We may drop the explicit \(\mathbf{x}\) from future expressions for simplicity.
\begin{align} p(\mathbf{y}|\mathbf{X},\mathbf{w}) \equiv p(\mathbf{y}|\mathbf{w}) = \prod_{i=1}^{n} \mathcal{N}\left(y_i|\mathbf{w}^\intercal \phi(\mathbf{x}_i), \beta^{-1} \right) \nonumber \end{align}
The corresponding conjugate prior \(p(\mathbf{w}| \alpha) = \mathcal{N}(\mathbf{w} | \mathbf{0}, \alpha^{-1}\mathbf{I})\). The posterior distribution is
\begin{align} p(\mathbf{w} | \mathbf{y}) & \propto p(\mathbf{y}|\mathbf{w}, \beta) p(\mathbf{w}) \nonumber \end{align}
The log of the posterior distribution takes the form
\begin{align*} \ln p(\mathbf{w} | \mathbf{y}, \mathbf{X}) &= \ln p(\mathbf{y}|\mathbf{w}, \beta) + \ln p(\mathbf{w})\\ &= \sum_{i=1}^{n} \ln \mathcal{N}\left(y_i|\mathbf{w}^\intercal \phi(\mathbf{x}_i), \beta^{-1} \right) + \ln \mathcal{N}(\mathbf{w} | \mathbf{0}, \alpha^{-1}\mathbf{I}) \\ &= -\frac{\beta}{2} \sum_{i=1}^{n} \left( y_i - \mathbf{w}^\intercal \phi(\mathbf{x}_i) \right)^2 - \frac{\alpha}{2} \mathbf{w}^\intercal \mathbf{w} + \text{const.} \nonumber \end{align*}
Moreover, we have \(p(\mathbf{w} | \mathbf{y}) = \mathcal{N}(\mathbf{w} | \mathbf{m}_n, \mathbf{S}_n)\).
We consider general prior \(p(\mathbf{w}) = \mathcal{N}(\mathbf{w} | \mathbf{m}_0, \mathbf{S}_0)\) and the posterior
\begin{align*} p(\mathbf{w} | \mathbf{y}) & \propto \left[ \prod_{i=1}^{n} \mathcal{N}\left(y_i|\mathbf{w}^\intercal \phi(\mathbf{x}_i), \beta^{-1} \right) \right] \mathcal{N}(\mathbf{w} | \mathbf{m}_0, \mathbf{S}_0) \\ & \propto \exp \left( -\frac{\beta}{2} (\mathbf{y} - \Phi \mathbf{w})^\intercal (\mathbf{y} - \Phi \mathbf{w})\right) \exp \left( -\frac{1}{2} (\mathbf{w} - \mathbf{m}_0)^\intercal \mathbf{S}^{-1}_0 (\mathbf{w} - \mathbf{m}_0)\right) \\ & = \exp \left[ -\frac{1}{2} \left(\mathbf{w}^\intercal (\mathbf{S}^{-1}_0 + \beta\Phi^\intercal \Phi ) \mathbf{w} - (\mathbf{S}^{-1}_0 \mathbf{m}_0 + \beta \Phi^\intercal \mathbf{y})^\intercal \mathbf{w} - \mathbf{w}^\intercal (\mathbf{S}^{-1}_0 \mathbf{m}_0 + \beta \Phi^\intercal \mathbf{y})\right) \right] \\ & \hspace{2cm} \exp \left[ -\frac{1}{2} \left( \beta \mathbf{y}^\intercal \mathbf{y} + \mathbf{m}_0^\intercal \mathbf{S}_0^{-1} \mathbf{m}_0\right) \right] \\ & = \exp \left( -\frac{1}{2} (\mathbf{w} - \mathbf{m}_n)^\intercal \mathbf{S}^{-1}_n (\mathbf{w} - \mathbf{m}_n)\right) \exp \left( -\frac{1}{2} (\beta \mathbf{y}^\intercal \mathbf{y} + \mathbf{m}_0^\intercal \mathbf{S}_0^{-1} \mathbf{m}_0 - \mathbf{m}_n^\intercal \mathbf{S}_n^{-1} \mathbf{m}_n)\right) \end{align*}
where
\begin{align*} \mathbf{m}_n = \mathbf{S}_n \left( \mathbf{S}^{-1}_0 \mathbf{m}_0 + \beta \mathbf{\Phi}^\intercal \mathbf{y} \right) \text{ and } \mathbf{S}^{-1}_n = \mathbf{S}^{-1}_0 + \beta \mathbf{\Phi}^\intercal \mathbf{\Phi} \end{align*}
The first exponential corresponds to the posterior, unnormalized Gaussian distribution over \(\mathbf{w}\), while the second exponential is independent of \(\mathbf{w}\) and hence can be absorbed into the normalization factor. For prior \(p(\mathbf{w}| \alpha) = \mathcal{N}(\mathbf{w} | \mathbf{0}, \alpha^{-1}\mathbf{I})\),
\begin{align} \mathbf{m}_n = \beta \mathbf{S}_n\mathbf{\Phi}^\intercal \mathbf{y} \text{ and } \mathbf{S}^{-1}_n = \alpha\mathbf{I} + \beta \mathbf{\Phi}^\intercal \mathbf{\Phi} \nonumber \end{align}
Bayesian Learning¶
We illustrate Bayesian learning and the sequential update of a posterior distribution on a simple example involving straight-line fitting.
Consider a simple linear model of the form \(y(x, \mathbf{w}) = -0.3 + 0.5 x\). We demonstrate how \(p(\mathbf{w} | \mathbf{y}, \mathbf{X})\) changes through learning
Figure “prior/posterior” shows the initial belief of \(\mathbf{w}\) and how it involves after knowing more data points. Based on Bayesian model, prior/posterior distribution is a normal distribution
multivariate_normal.pdf(w, mean=model.w_mean, cov=model.w_cov)and the mean is approaching to the true value \((-.3, .5)\) from \((0,0)\).
The likelihood function provides a soft constraint that the line must pass close to the data point, where close is determined by the noise precision \(\beta\). We demonstrate \(p(y_0|x_0, \mathbf{w})\) for one point (at
endposition). Standardized pdfcontour(w0, w1, multivariate_normal.pdf((-t_train[end-1: end] + w @ phi_train[end-1: end].T)*model.beta))enumerates all the values of \(\mathbf{w}\) and shows the probability that the response \(y_0\) occurs. The graph always highlights a straight stripe near the true value \((-.3, .5)\) because any \(\mathbf{w}\) on the line \(y_0 = w_0 + w_1 x_0\) has large likelihood function value.
The lines in Figure “data space” are based on randomly generated \(\mathbf{w}\) following current belief.
[38]:
def linear(x):
return -0.3 + 0.5 * x
w0, w1 = np.meshgrid(
np.linspace(-1, 1, 100),
np.linspace(-1, 1, 100))
w = np.array([w0, w1]).transpose(1, 2, 0)
x_train, t_train = create_data(linear, 20, 0.1, [-1, 1])
x_test = np.linspace(-1, 1, 100)
phi_train = Polynomial(1).dm(x_train)
phi_test = Polynomial(1).dm(x_test)
model = Bayesian(alpha=2., beta=25.)
for beg, end in [[0, 0], [0, 1], [1, 2], [2, 3], [3, 20]]:
model.fit(phi_train[beg: end], t_train[beg: end])
fig, axes = plt.subplots(1,3,figsize=(16, 4))
if end > 0:
axes[0].scatter(-0.3, 0.5, s=200, marker="x")
# Use standardization.
axes[0].contour(w0, w1,
multivariate_normal.pdf((-t_train[end-1: end] + w @ phi_train[end-1: end].T)*model.beta))
axes[0].set_xlabel("$w_0$")
axes[0].set_ylabel("$w_1$")
axes[0].set_title("likelihood")
axes[1].scatter(-0.3, 0.5, s=200, marker="x")
axes[1].contour(w0, w1, multivariate_normal.pdf(w, mean=model.w_mean, cov=model.w_cov))
axes[1].set_xlabel("$w_0$")
axes[1].set_ylabel("$w_1$")
axes[1].yaxis.set_label_coords(-.12,.5)
axes[1].set_title("prior/posterior")
axes[2].scatter(x_train[:end], t_train[:end], s=20, facecolor="none", edgecolor="steelblue", lw=1)
# use posterior dist to generate w, and then w is used for prediction
axes[2].plot(x_test,
phi_test @ np.random.multivariate_normal(model.w_mean, model.w_cov, size=6).T, c="orange")
axes[2].set_xlim(-1, 1)
axes[2].set_ylim(-1, 1)
axes[2].set_xlabel("$x$")
axes[2].set_ylabel("$y$")
axes[2].yaxis.set_label_coords(-.12,.5)
axes[2].set_title(r"data space $n={}$".format(end))
plt.show()
toggle()
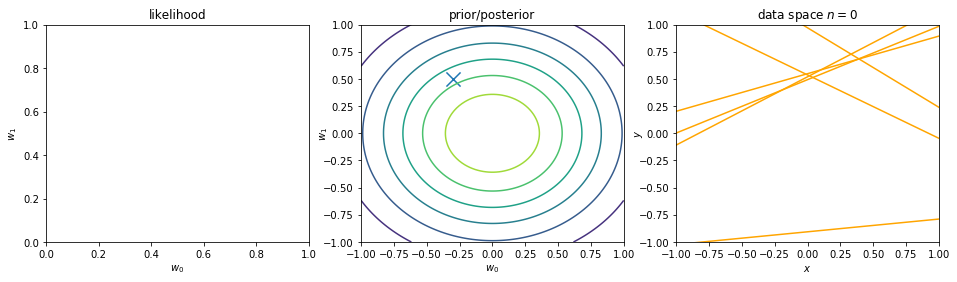




[38]:
Bayesian Prediction¶
We use polynomial curve fitting as an illustration of the predictive distribution for Bayesian linear regression models. It provides a confidence region on predictions
[39]:
x_train, t_train = create_data(sinusoidal, 10, 0.25)
x_test = np.linspace(0, 1, 100)
t_test = sinusoidal(x_test)
phi_train = Gaussian(np.linspace(0, 1, 9), 0.1).dm(x_train)
phi_test = Gaussian(np.linspace(0, 1, 9), 0.1).dm(x_test)
t, t_std = Bayesian(alpha=2e-3, beta=2).fit(phi_train, t_train).predict_dist(phi_test)
plt.scatter(x_train, t_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, t_test, c="g", label="$\sin(2\pi x)$")
plt.plot(x_test, t, c="r", label="mean")
plt.fill_between(x_test, t_test - t_std, t_test + t_std, color="pink", label="std.", alpha=0.5)
plt.xlim(-0.1, 1.1)
plt.ylim(-1.5, 1.5)
plt.annotate("n=9", xy=(0.8, 1))
plt.legend(bbox_to_anchor=(1.05, 1.), loc=2, borderaxespad=0.)
plt.show()
toggle()
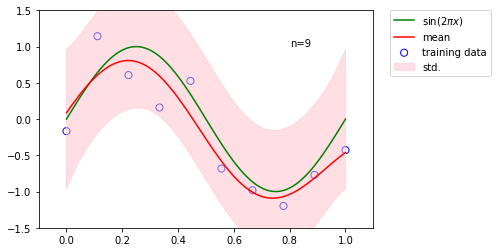
[39]:
To recap the example and dive into the details, we show the predictive distribution for Bayesian linear regression models by sequentially learning data points.
[40]:
x_train, t_train = create_data(sinusoidal, 25, 0.25)
x_test = np.linspace(0, 1, 100)
t_test = sinusoidal(x_test)
phi_train = Gaussian(np.linspace(0, 1, 9), 0.1).dm(x_train)
phi_test = Gaussian(np.linspace(0, 1, 9), 0.1).dm(x_test)
model = Bayesian(alpha=2e-3, beta=2)
plt.figure(figsize=(18, 8))
for i, [beg, end] in enumerate([[0, 1], [1, 2], [2, 4], [4, 8], [8, 25]]):
t, t_std = model.fit(phi_train[beg: end], t_train[beg: end]).predict_dist(phi_test)
plt.subplot(2,3,i+1)
plt.scatter(x_train[:end], t_train[:end], s=100, facecolor="none", edgecolor="steelblue", lw=2)
plt.plot(x_test, t_test, label="$\sin(2\pi x)$")
plt.plot(x_test, t, label="fitting")
plt.fill_between(x_test, t - t_std, t + t_std, color="orange", alpha=0.5)
plt.xlim(-0.02, 1)
plt.ylim(-2, 2)
plt.title(r"data size $n={}$".format(end))
plt.legend()
plt.show()
toggle()
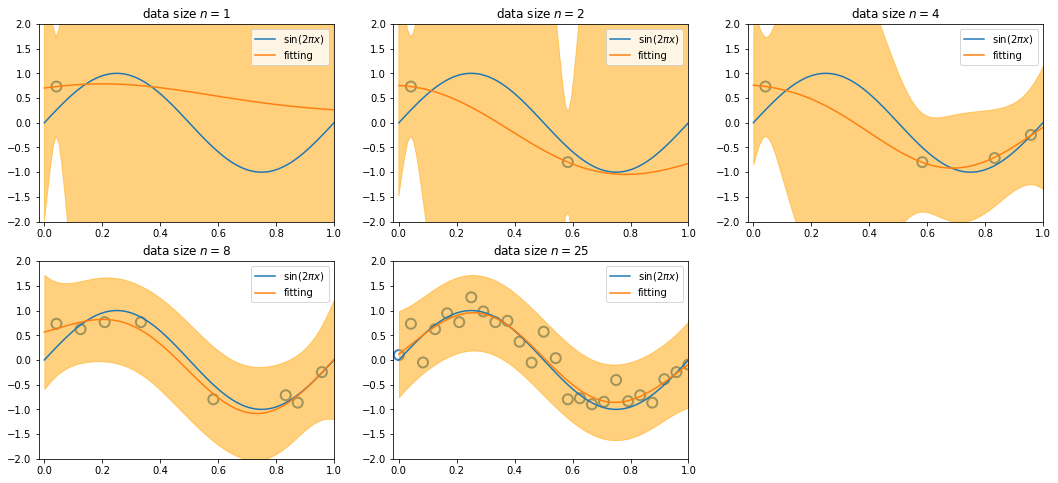
[40]:
Evidence Approximation¶
The predictive distribution is \begin{align} p(t|\mathbf{y}, \alpha, \beta) = \mathcal{N} \left( t | \mathbf{m}^\intercal_{n} \phi(\mathbf{x}), \sigma^2_n(\mathbf{x}) \right) \nonumber \end{align}
The key is to obtain hyperparameters \(\alpha, \beta\) as well as \(\mathbf{m}_n\).
Initialization: \(k = 0\), \(\alpha^0 = \alpha_0\) and \(\beta^0 = \beta_0\)
Find eigenvalues \(\lambda_i\), \(i=0, \ldots, M-1\) such that \begin{align} \left(\beta \Phi^\intercal \Phi \right) \mathbf{u}_i = \lambda_i \mathbf{u}_i \nonumber \end{align}
- Let\begin{align} \gamma^k = \sum_{i=0}^{M-1} \frac{\lambda_i}{\alpha^k+\lambda_i},~ \alpha^{k+1} = \frac{\gamma^k}{\mathbf{w}^\intercal_{mean} \mathbf{w}_{mean}} \text{ and } \frac{1}{\beta^{k+1}} = \frac{1}{N - \gamma} \sum_{i=1}^{N} \left( y_i - \mathbf{w}^\intercal_{mean} \phi(x_i) \right)^2 \nonumber \end{align} where \(\mathbf{w}_{mean} = \mathbf{m}_n = \beta \mathbf{S}_n\mathbf{\Phi}^\intercal \mathbf{y}\).
If \(|\alpha^{k+1} - \alpha^{k}| + |\beta^{k+1} - \beta^{k}| <\) threshold, then return \(\alpha, \beta\), else \(k = k+1\) and go to step 2.
For the polynomial regression model with degree from 0 to 8, we find the optimal value of the evidence function. The empirical bayes approach is applied and the evidence favours the model with degree \(= 3\).
[41]:
def cubic(x):
return x * (x - 5) * (x + 5)
x_train, t_train = create_data(cubic, 30, 10, [-5, 5])
x_test = np.linspace(-5, 5, 100)
t_test = cubic(x_test)
phi_train = [Polynomial(i).dm(x_train) for i in range(8)]
models = [Empirical(alpha=100., beta=100.).fit(phi, t_train, max_iter=100) for phi in phi_train]
evidences = [model.log_evidence(phi, t_train) for model, phi in zip(models, phi_train)]
opt_degree = int(np.nanargmax(evidences))
phi_test = Polynomial(opt_degree).dm(x_test)
t, t_std = models[opt_degree].predict_dist(phi_test)
plt.scatter(x_train, t_train, s=50, facecolor="none", edgecolor="steelblue", label="observation")
plt.plot(x_test, t_test, label="x(x-5)(x+5)")
plt.plot(x_test, t, label="prediction")
plt.fill_between(x_test, t - t_std, t + t_std, alpha=0.5, label="std", color="orange")
plt.legend()
plt.show()
plt.plot(evidences)
plt.title("Model evidence")
plt.xlabel("degree")
plt.ylabel("log evidence")
plt.show()
toggle()
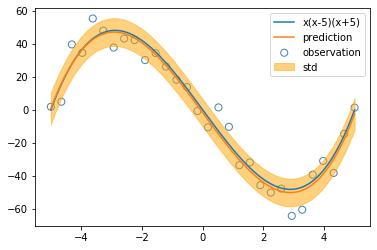
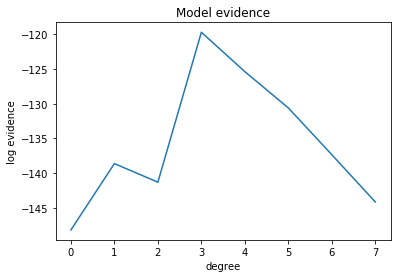
[41]: