[1]:
%run ../initscript.py
HTML("""
<div id="popup" style="padding-bottom:5px; display:none;">
<div>Enter Password:</div>
<input id="password" type="password"/>
<button onclick="done()" style="border-radius: 12px;">Submit</button>
</div>
<button onclick="unlock()" style="border-radius: 12px;">Unclock</button>
<a href="#" onclick="code_toggle(this); return false;">show code</a>
""")
[1]:
[2]:
# import pandas as pd
# import numpy as np
# import matplotlib.pyplot as plt
# from matplotlib.path import Path
# from matplotlib.patches import PathPatch
# import seaborn as sns
# # from pulp import *
# from ipywidgets import *
# %matplotlib inline
# import warnings
# warnings.filterwarnings('ignore')
%run ./loadoptfuncs.py
toggle()
[2]:
Mixed-Integer Programming¶
Optimization models in which some or all of the variables must be integer are known as mixed-integer programming (MIP). There are two main reasons for using MIP.
The decision variables are quantities that have to be integer, e.g., number of employee to assign or number of car to make
The decision variables are binaries to indicate whether an activity is undertaken, e.g., \(z=0\) or \(1\) where \(1\) indicates the decision of renting an equipment so that the firm need to pay a fixed cost, \(0\) otherwise.
If we relax the integrality requirements of MIP, then we obtain a so-called LP relaxation of a given MIP.
You might suspect that MIP would be easier to solve than LP models. After all, there are only a finite number of feasible integer solutions in an MIP model, whereas there are infinitely many feasible solutions in an LP model.
However, exactly the opposite is true. MIP models are considerably harder than LP models, because the optimal solution rarely occurs at the corner of its LP relaxation. Algorithms such as Branch-and-bound (B&B) or Branch-and-cut (B&C) are designed for solving MIP effectively and well implemented in commercial software.
Branch and Bound Algorithm¶
Branch-and-bound algorithm is designed to use LP relaxation to solve MIP. The picture shows the difference between a MIP and its LP relaxation.
The “integer feasible region” in the picture connects all integer feasible solutions. In particular, it is a convex combination of all feasible solutions.
Similar to LP, the optimal solution of the MIP occurs at the corner of the integer feasible region.
However, as shown in the picture, the boundary of integer feasible region is much more complicated than its LP relaxation feasible region.
[3]:
show_integer_feasregion()
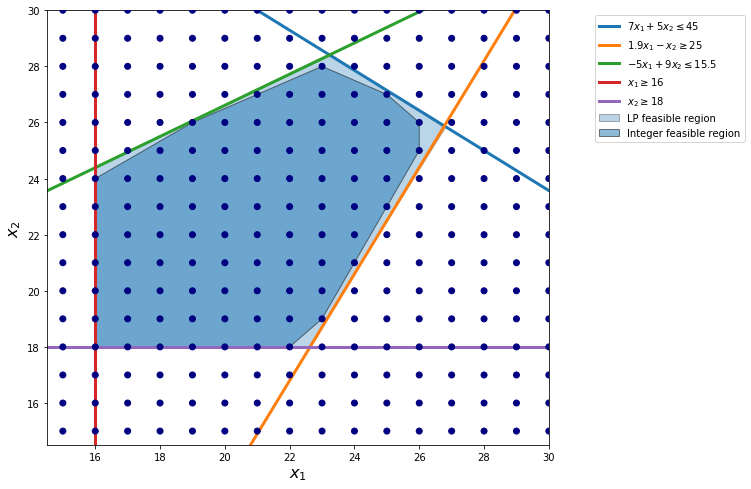
We demonstrate branch-and-bound procedure as follows.
[4]:
from ipywidgets import widgets
from IPython.display import display, Math
from traitlets import traitlets
class LoadedButton(widgets.Button):
"""A button that can holds a value as a attribute."""
def __init__(self, value=None, *args, **kwargs):
super(LoadedButton, self).__init__(*args, **kwargs)
# Create the value attribute.
self.add_traits(value=traitlets.Any(value))
def add_num(ex):
ex.value = ex.value+1
if ex.value<=3:
fig, ax = plt.subplots(figsize=(9, 8))
ax.set_xlim(15-0.5, 30)
ax.set_ylim(15-0.5, 30)
s = np.linspace(0, 50)
plt.plot(s, 45 - 5*s/7, lw=3, label='$5x_1 + 7x_2 \leq 315$')
plt.plot(s, -25 + 1.9*s, lw=3, label='$1.9x_1 - x_2 \leq 25$')
plt.plot(s, 15.5 + 5*s/9, lw=3, label='$-5x_1 + 9x_2 \leq 139.5$')
plt.plot(16 * np.ones_like(s), s, lw=3, label='$x_1 \geq 16$')
plt.plot(s, 18 * np.ones_like(s), lw=3, label='$x_2 \geq 18$')
# plot the possible (x1, x2) pairs
pairs = [(x1, x2) for x1 in np.arange(start=15, stop=31, step=1)
for x2 in np.arange(start=15, stop=31, step=1)]
# split these into our variables
x1, x2 = np.hsplit(np.array(pairs), 2)
# plot the results
plt.scatter(x1, x2, c=0*x1 - 0*x2, cmap='jet', zorder=3)
feaspairs = [(x1, x2) for x1 in np.arange(start=15, stop=31, step=1)
for x2 in np.arange(start=15, stop=31, step=1)
if (5/7*x1 + x2) <= 45
and (-1.9*x1 + x2) >= -25
and (-5/9*x1 + x2) <= 15.5
and x1>=16 and x2>=18]
# split these into our variables
x1, x2 = np.hsplit(np.array(feaspairs), 2)
# plot the results
plt.scatter(x1, x2, c=5*x1 - 6*x2, label='Profit = $5x_1 - 6x_2$', cmap='jet', zorder=3)
if ex.value>=3:
bpath1 = Path([
(16., 18.),
(16., 24.4),
(22, 27.8),
(22, 27),
(22, 18.),
(16., 18.),
])
bpatch1 = PathPatch(bpath1, label='New feasible region', alpha=0.5)
ax.add_patch(bpatch1)
bpath2 = Path([
(23., 18.7),
(23., 28.2),
(23.2,28.4),
(26.8, 25.8),
(23., 18.7),
])
bpatch2 = PathPatch(bpath2, label='New feasible region', alpha=0.5)
ax.add_patch(bpatch2)
cb = plt.colorbar()
cb.set_label('profit', fontsize=14)
plt.xlim(15-0.5, 30)
plt.ylim(15-0.5, 30)
plt.xlabel('$x_1$', fontsize=16)
plt.ylabel('$x_2$', fontsize=16)
lppath = Path([
(16., 18.),
(16., 24.4),
(23.3, 28.4),
(26.8, 25.8),
(22.6, 18.),
(16., 18.),
])
lppatch = PathPatch(lppath, label='LP feasible region', alpha=0.3)
ax.add_patch(lppatch)
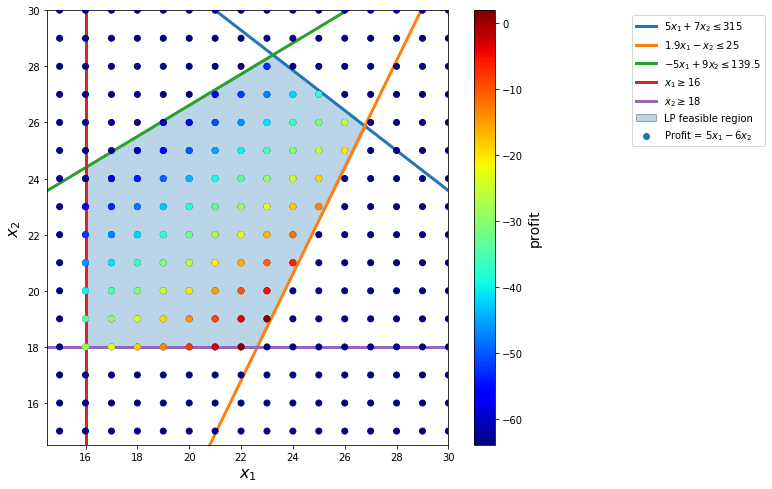
if ex.value==1:
display(Math('Show~feasible~region...'))
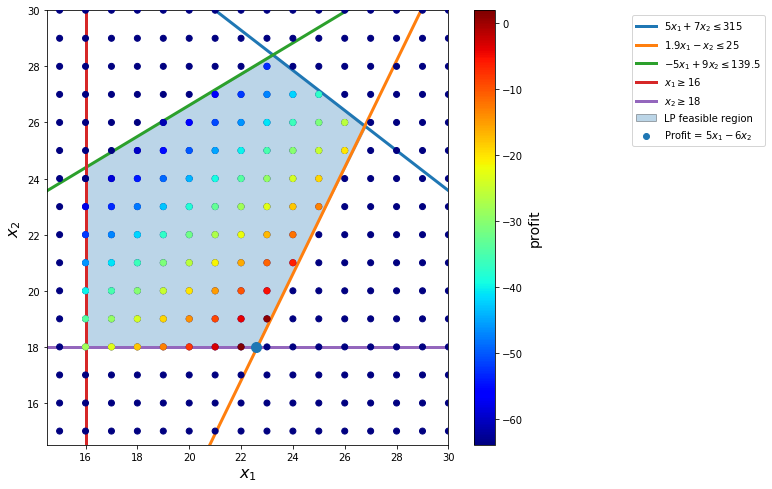
if ex.value==2:
display(Math('Solve~linear~programming...'))
display(Math('\nThe~solution~is~x_1 = {:.3f}, x_2={}~with~profit={}'.format(22.632,18,5.158)))
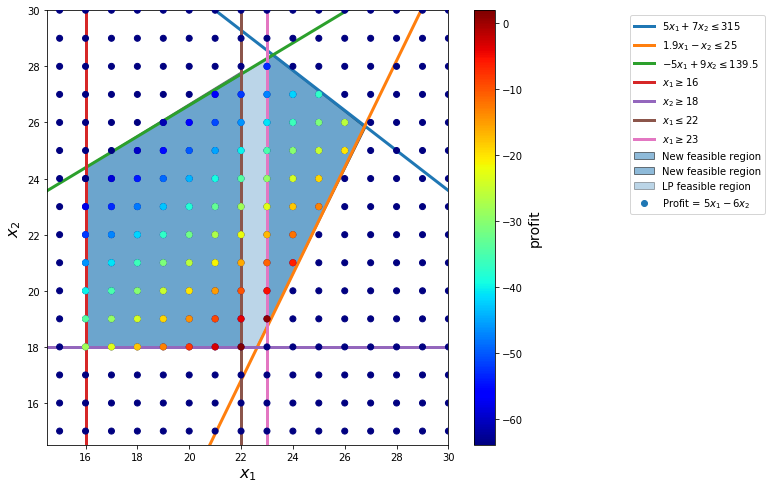
if ex.value==3:
display(Math('The~solution~is~integer~infeasible.~So~we~use~branch~and~bound.'))
display(Math('Branch~LP~feasible~region~into~two:~x_1 \le 22~and~x_1 \ge 23,~and~solve~two~LPs.'))
display(Math('Bound~the~optimal~profit~from~above~with~5.158.'))
if ex.value==2:
plt.scatter([22.57], [18], s=[100], zorder=4)
if ex.value>=3:
plt.plot(22 * np.ones_like(s), s, lw=3, label='$x_1 \leq 22$')
plt.plot(23 * np.ones_like(s), s, lw=3, label='$x_1 \geq 23$')
plt.legend(fontsize=18)
ax.legend(loc='upper right', bbox_to_anchor=(1.8, 1))
plt.show()
# lb = LoadedButton(description="Next", value=0)
# lb.on_click(add_num)
# display(lb)
class ex:
value = 1
for i in range(3):
ex.value = i
add_num(ex)
toggle()
[4]:
The Branch-and-bound algorithm keeps a tree structure in its solving process.
Modeling with Binary Variables¶
A binary variable usually corresponds to an activity that is or is not undertaken. We can model logics by using constraints involving binary variables.
For example, let \(z_1, \ldots, z_5\) be variables to indicate whether we will order products from suppliers \(1, \ldots, 5\) respectively.
The logic “if you use supplier 2, you must also use supplier 1” can be modeled as
\begin{align} z_2 \le z_1 \nonumber \end{align}
The logic “if you use supplier 4, you may NOT use supplier 5” can be modeled as
\begin{align} z_4 + z_5 \le 1 \nonumber \end{align}
Example: Facility Location¶
Consider the classic facility location problem. Given
a set \(L\) of customer locations and
a set \(F\) of candidate facility sites
We must decide on which sites to build facilities and assign coverage of customer demand to these sites so as to minimize cost.
All customer demand \(d_ i\) must be satisfied, and each facility has a demand capacity limit \(C\).
The total cost is the sum of the distances \(c_{ij}\) between facility \(j\) and its assigned customer \(i\), plus a fixed charge \(f_ j\) for building a facility at site \(j\).
Let \(y_ j = 1\) represent choosing site \(j\) to build a facility, and 0 otherwise. Also,
let \(x_{ij} = 1\) represent the assignment of customer \(i\) to facility \(j\), and 0 otherwise.
This model can be formulated as the following integer linear program:
Constraint (2) ensures that each customer is assigned to exactly one site.
Constraint (3) forces a facility to be built if any customer has been assigned to that facility.
Finally, constraint (4) enforces the capacity limit at each site.
\begin{align} \min & \quad \sum_{i \in L} \sum_{j \in F} c_{ij} x_{ij} + \sum_{j \in F} f_j y_j \\ \text{s.t.} & \quad \sum_{j \in F} x_{ij} = 1 && \forall i \in L \\ & \quad x_{ij} \leq y_j && \forall i \in L, j \in F \\ & \quad \sum_{i \in L} d_i x_{ij} \le C y_j && \forall j \in F \\ & \quad x_{ij} \in \{0,1\}, y_j \in \{0,1\} && \forall i \in L, j \in F \end{align}
SAS Log for MIP
NOTE: The Branch and Cut algorithm is using up to 2 threads.
Node Active Sols BestInteger BestBound Gap Time
0 1 5 13138.9827130 0 13139 0
0 1 5 13138.9827130 9946.2514269 32.10% 0
0 1 5 13138.9827130 9964.0867656 31.86% 0
0 1 5 13138.9827130 9972.4224200 31.75% 0
0 1 7 11165.8124056 9975.2866538 11.93% 0
0 1 7 11165.8124056 9977.8057106 11.91% 0
0 1 7 11165.8124056 9978.9372347 11.89% 0
0 1 7 11165.8124056 9980.8568737 11.87% 0
0 1 9 10974.7644641 9982.4953533 9.94% 0
NOTE: The MILP solver added 17 cuts with 492 cut coefficients at the root.
100 37 10 10961.8123535 10380.2158229 5.60% 0
121 44 11 10954.3760034 10938.0514190 0.15% 0
131 48 12 10951.0805543 10941.1165997 0.09% 0
139 49 13 10948.4603465 10941.1165997 0.07% 0
187 8 13 10948.4603465 10947.3813808 0.01% 0
NOTE: Optimal within relative gap.
NOTE: Objective = 10948.460347.
Although a MIP problem sometimes can be difficult to solve to its optimality, the gap column provides us useful information on solution quality. It shows that the objective value of the best integer solution the solver find so far is within a certain percentage gap of the true underlying optimal solution.